Im letzten Beitrag hatte ich (externer Link) Daten des Economist quantitativ ausgewertet. Das Wirtschaftswachstum, betrachtet seit dem Zweiten Weltkrieg und für alle neun Präsidenten, die sich bis dato einer Wiederwahl gestellt hatten, legte nahe, dass es für Obama sehr eng werden würde. Der hat die Wahl nun aber gewonnen. Außergewöhnliches Glück? Oder Ergebnis einer (externer Link) „Analytics“-Strategie? Meine Auswertung der Daten ergab, dass Obamas Chancen rein rechnerisch bei 6% hätten liegen sollen. Lässt sich daraus im Umkehrschluss ableiten, dass sein Sieg mit 94% Wahrscheinlichkeit an besonderen Umständen wie „Analytics“ gelegen hat?

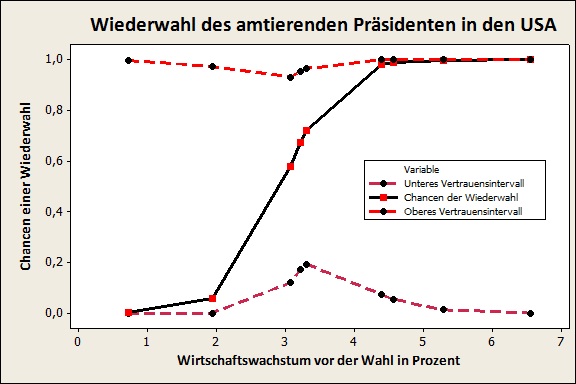
Der Schluss wäre falsch. Die entscheidende Frage lautet: wie sicher sind diese 6%, wie gut ist das Vertrauensintervall dafür? Legt man ein 95%-Vertrauensintervall zugrunde,
dann ist das „Signal“, das wir in der Graphik zu sehen geglaubt hatten, nichts
als eine „Fata Morgana“. Uns ist ein „Typ-I“ Fehler unterlaufen: mit 95% Wahrscheinlichkeit liegt die Chance der Wiederwahl lediglich „irgendwo zwischen 0 und 100 Prozent“. Wir müssten also über Daten von deutlich mehr Wahlergebnissen verfügen, um diesen Zusammenhang zu ermitteln – so er denn besteht.

Was lehrt uns das? Die im letzten Beitrag getroffene Aussage ist noch dringlicher: wir können uns Daten anschauen, wie wir möchten, um Hypothesen zu bilden („die Wiederwahl des amtierenden Präsidenten könnte vom Wirtschaftswachstum abhängen“). Danach müssen wir aber ein valides Verfahren verwenden, um diese Hypothese quantitativ zu prüfen. Oder wir werden immer wieder einen der beiden Fehler begehen und entweder einer Fata Morgana aufsitzen oder aber ein wichtiges
Signal übersehen.

Recherisch bestimmte Wahrscheinlichkeit der Wiederwahl und Vertrauensintervall dafür

Anmerkung für Kenner von „Minitab“: diesen Graph erhält man über Stat > Regression > Binary Logistic Regression. Dort dann unter „Prediction“ das Abspeichern von Ereigniswahrscheinlichkeit und Vertrauensintervallen anwählen. Diese Ergebnisse lassen sich dann mittels „Scatterplot“ darstellen.