Ich werde mehr und mehr ein Fan der – zunächst unhandlich erscheinenden – Programmiersprache R. Wie vieles andere, so stehen dort längst auch die von Hans Rosling und der Gapminder-Foundation entwickelten Werkzeuge zur dynamischen Visualisierung von Daten zur Verfügung. Wir können damit die weltweite Entwicklung der Corona-Fälle als animierte gif-Datei visualisieren.

Dargestellt sind wieder die auf Github abgelegten Daten der Johns Hopkins Universität. Die Größe eines Punktes stellt dabei den Krankenstand dar und die Farbe die Rate der Veränderung (für die wir fünf Kategorien verwenden). Für die USA sind separate Datensätze auf regionaler Ebene vorhanden – jedoch leider nur für die bestätigten und die Todesfälle, nicht jedoch für die Anzahl der Genesenen. Da wir uns hier für den Krankenstand interessieren, verwenden wir die Daten für das gesamte Land.

Nachdem in Deutschland und vielen anderen Ländern über Wochen hinweg die Zahl der bestätigten Corona-Fälle exponentiell gestiegen ist und sich in zwei bis drei Tagen verdoppelt hat, zeigen die Maßnahmen inzwischen deutliche Wirkung: das exponentielle Wachstum konnte auf ein lineares heruntergebremst werden.

Wir sehen uns für ausgewählte Länder den verfügbaren Datensatz an:

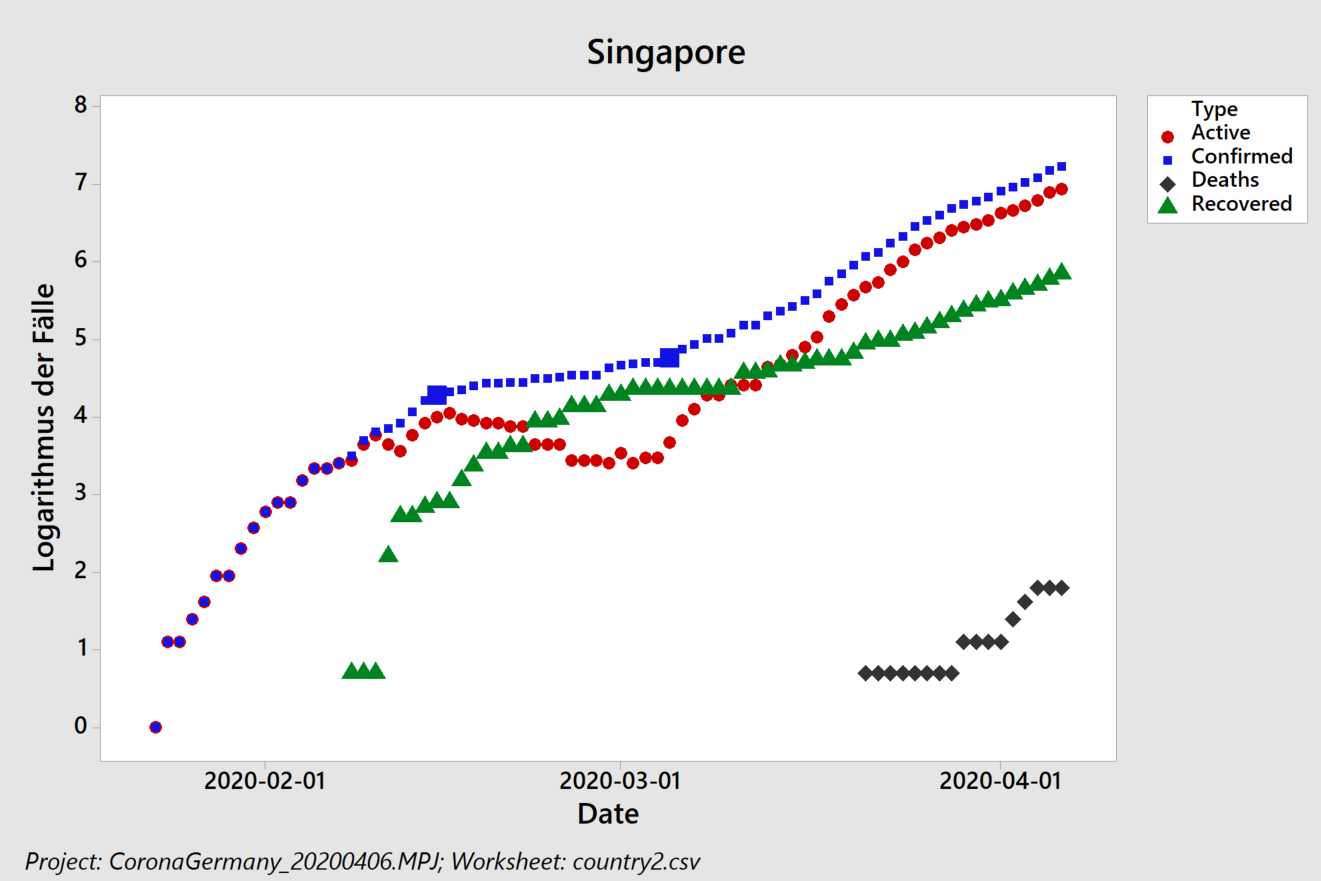
Zunächst fällt auf, dass die Lage in Singapur sich verschlimmert hat – wir hatten den Stadtstaat als „Ausnahmefall“ diskutiert und empfohlen, sich von dort Ideen zu holen. Wie deutsche Zeitungen berichten, ist allerdings inzwischen unter eng zusammenlebenden ausländischen Arbeitskräften Corona erneut ausgebrochen und gelangt von dort auch zur übrigen Bevölkerung.

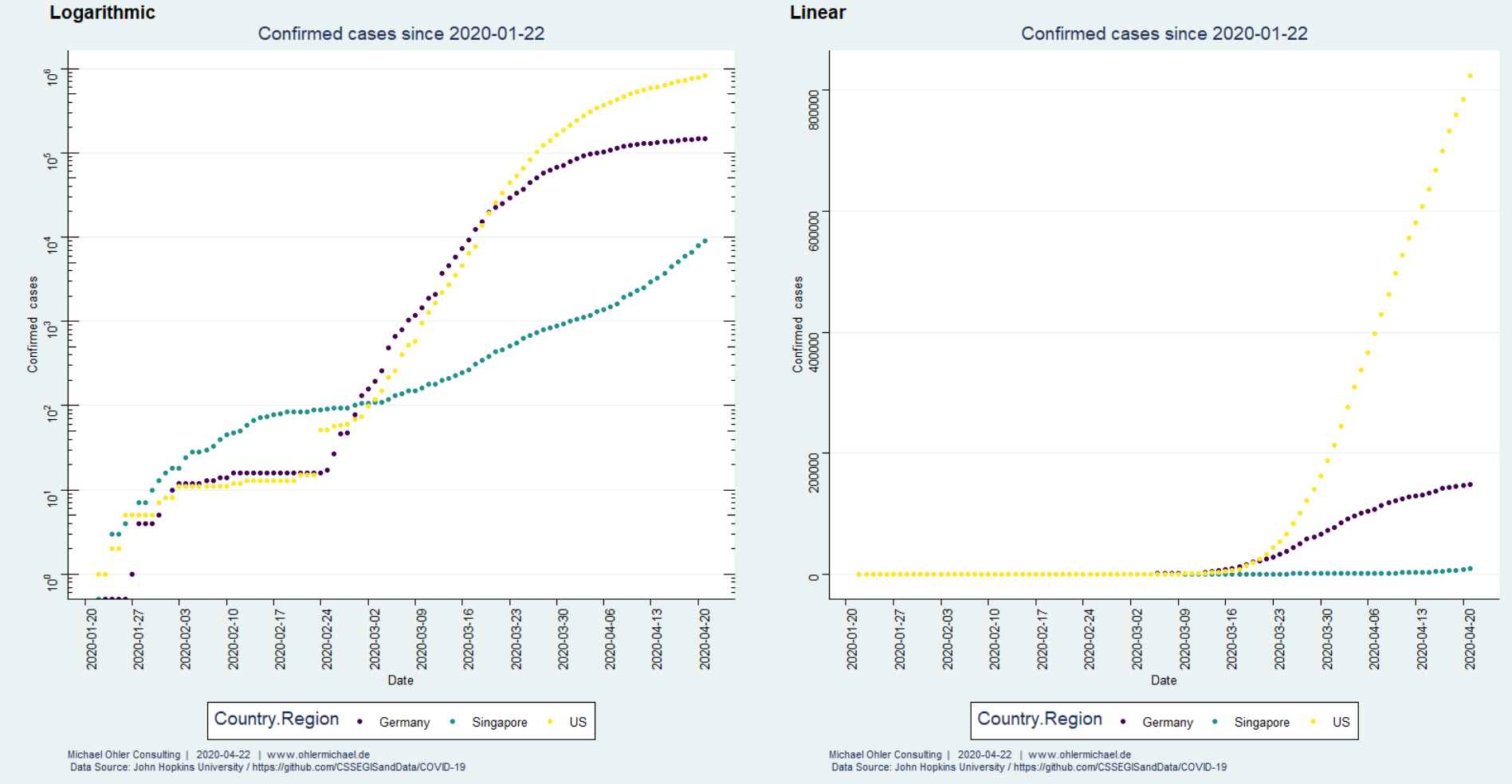
Am anderen Ende der Skala fällt auf, dass in den USA die bestätigten Fälle ab ca. dem 3. Februar exponentiell angestiegen sind (was in logarithmischer Auftragung zu einer Geraden führt) aber seit ca. dem 27. März linear wachsen.

Wir wollen nun die Ausbreitung von Corona in diesen Ländern miteinander vergleichen. Dazu betrachten wir den Zeitraum ab dem 300sten bestätigten Fall.

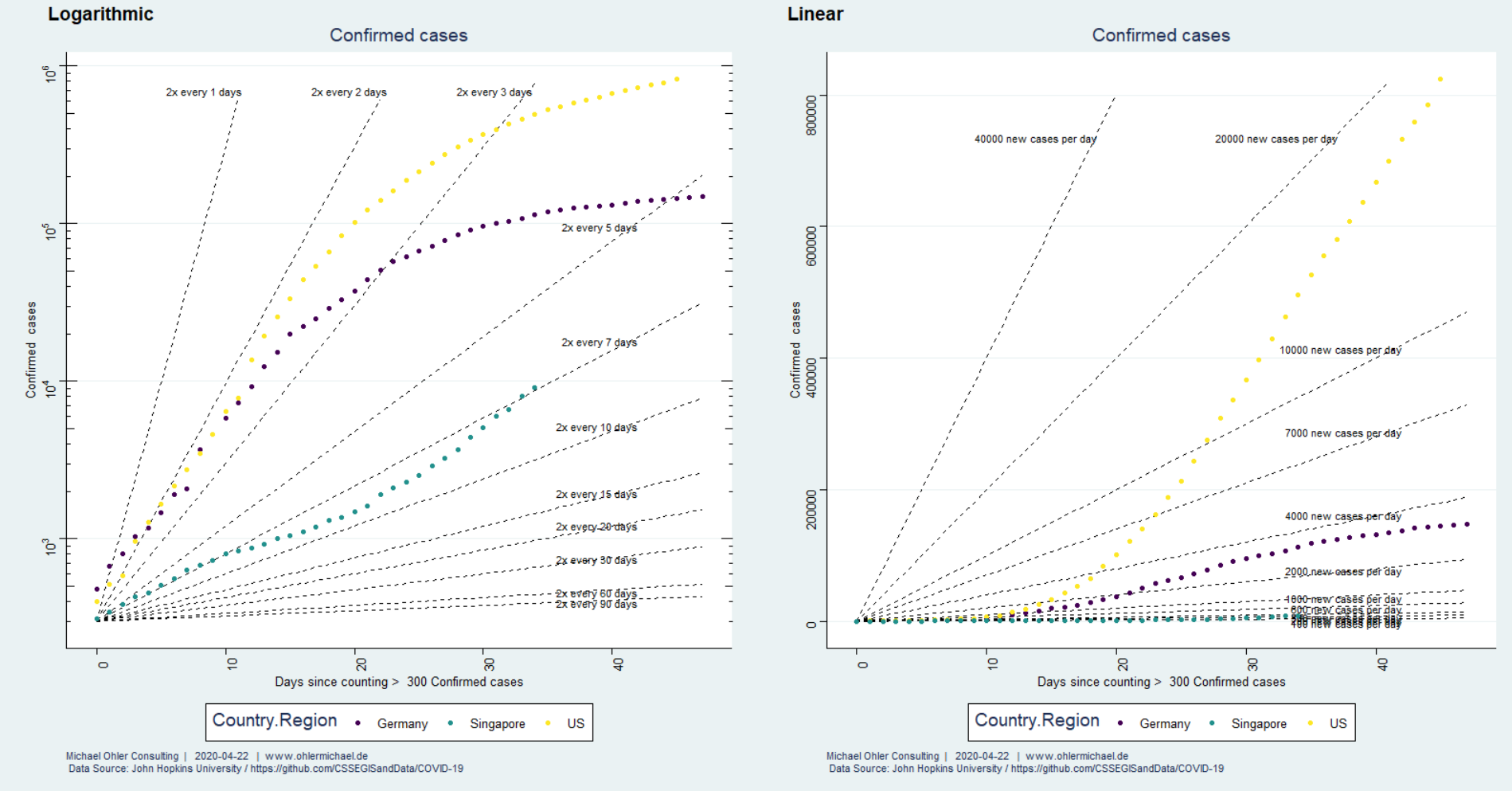
So fällt auf, dass das exponentielle Wachstum in Deutschland und den USA zunächst sehr ähnlich verlief (wie auch in Spanien, Italien und vielen anderen Länder, wir haben das in früheren Beiträgen diskutiert). In Deutschland gelingt es dann jedoch, dieses Wachstum nach ca. 2 Wochen sichtbar zu bremsen. Der Vergleich der rechten und der linken Darstellung erlaubt zu erkennen, über welche Zeiträume hinweg das Wachstum eher exponentiell und wann es linear verläuft. Wir schauen uns diese Dinge unten genauer an.

Vorteile eines linearen Anstiegs der bestätigten Fälle

Bei einem exponentiellen Wachstum mit einer Verdopplungszeit von 3 Tagen haben wir nach 3 Tagen doppelt so viele Fälle, nach 6 Tagen schon viermal so viele, nach neun Tagen achtmal – und so weiter, bis das Gesundheitssystem zusammenbricht.

Für ein lineares Wachstum kommt dagegen jeden Tag in etwa die gleiche Anzahl neuer Fälle hinzu. Die Situation wird dadurch handhabbar, wie man über das Gesetz von Little erkennt: bei 2000 neuen Fällen Tag für Tag und falls Menschen im Mittel 30 Tage lang krank bleiben, dann muss das Gesundheitssystem einen mehr oder weniger konstanten Krankenstand von etwa 2000*30 = 60000 bewältigen. Bei bekanntem Prozentsatz  schwerer Fälle lässt sich so nicht zuletzt der Bedarf an Beatmungsgeräten planen. Für ein exponentielles Wachstum steigt dieser Bedarf dagegen exponentiell an.

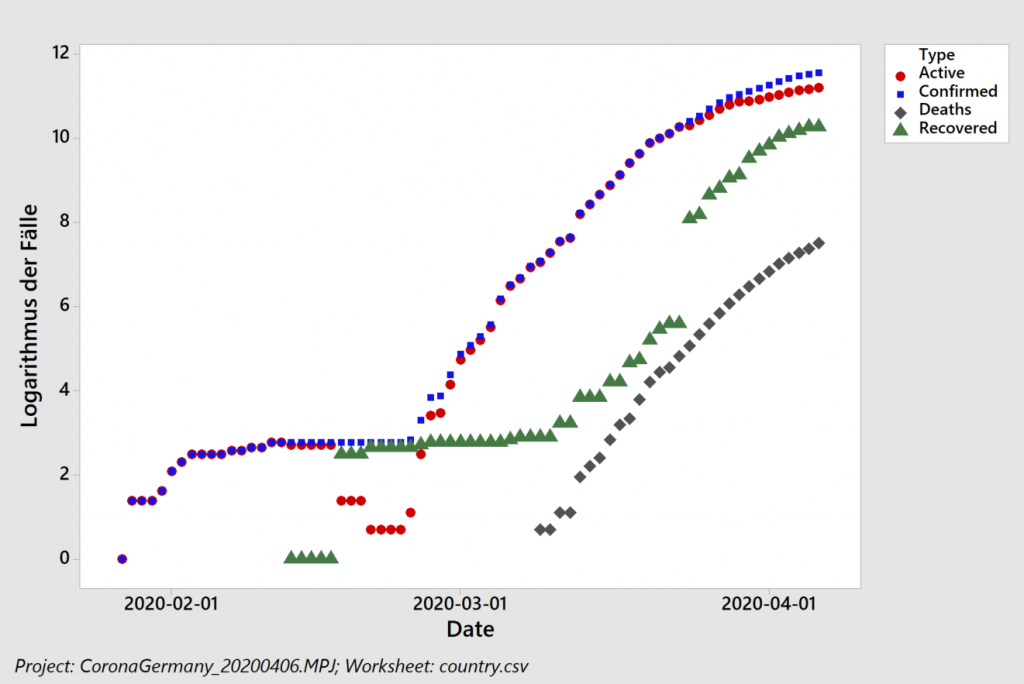
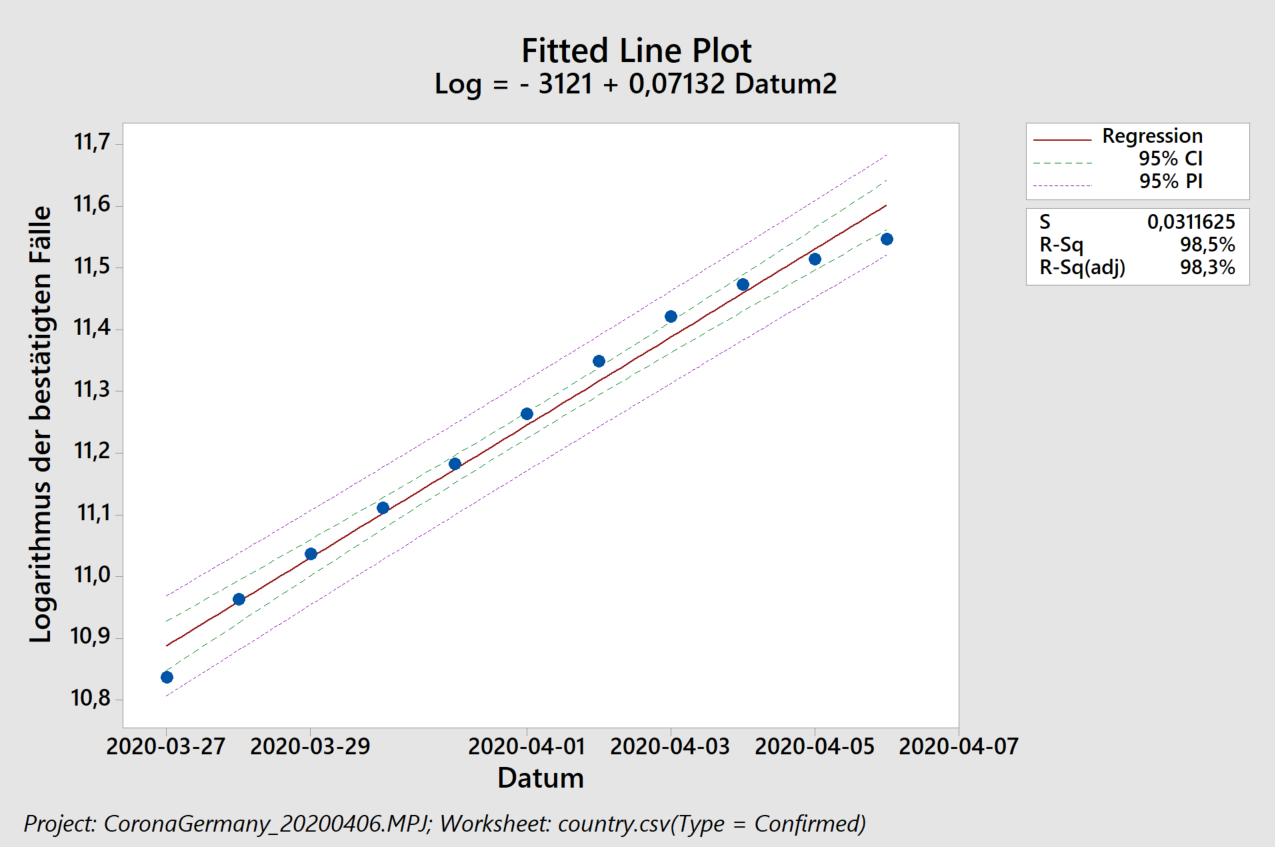
Wie sieht die Lage in Deutschland aus?

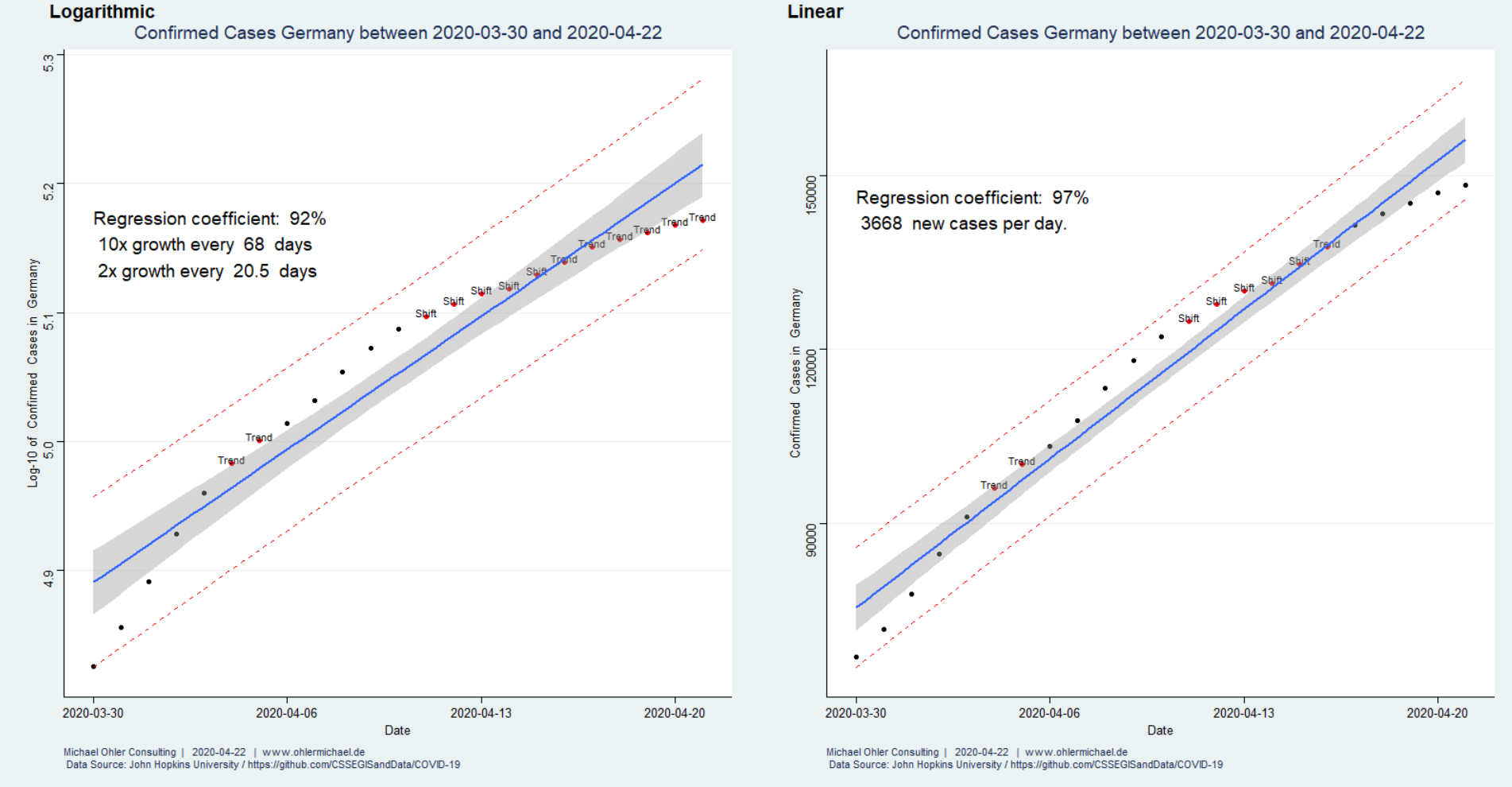
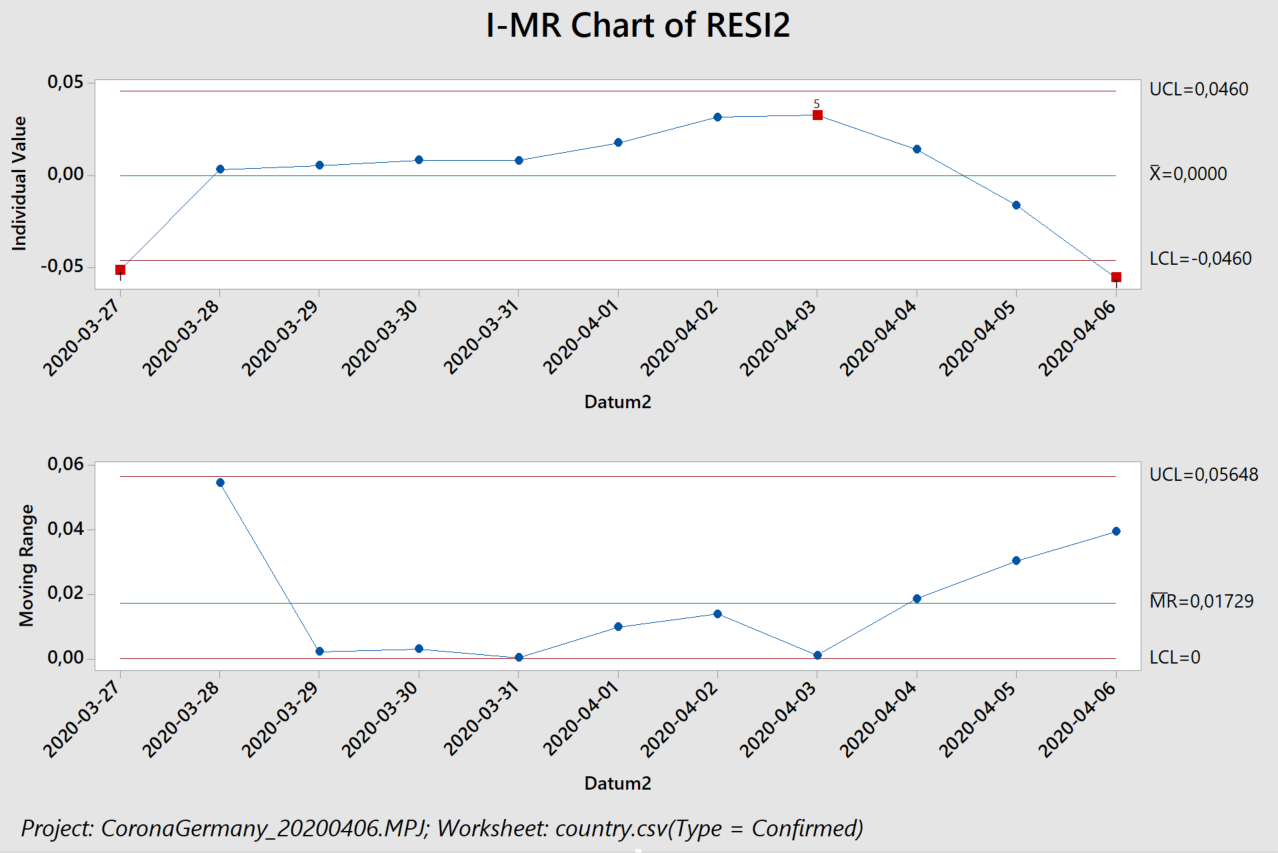
Wir haben die „Western Electric“ oder „Nelson“ Regeln, die wir im letzten Beitrag noch in Minitab verwendet haben, inzwischen in unser R-Programm übertragen (Ayush aus Indien sei Dank dafür, den Fehler in meinem Code gefunden zu haben).

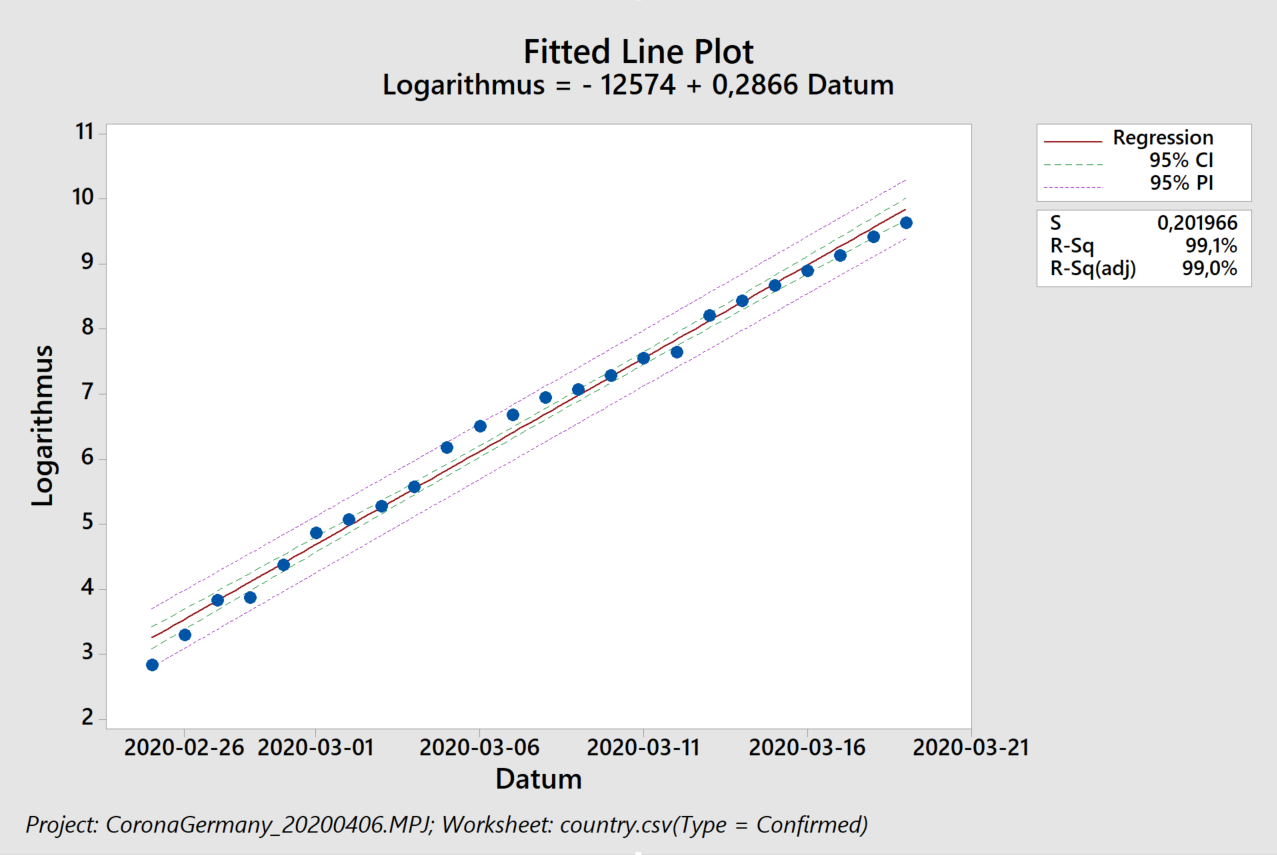
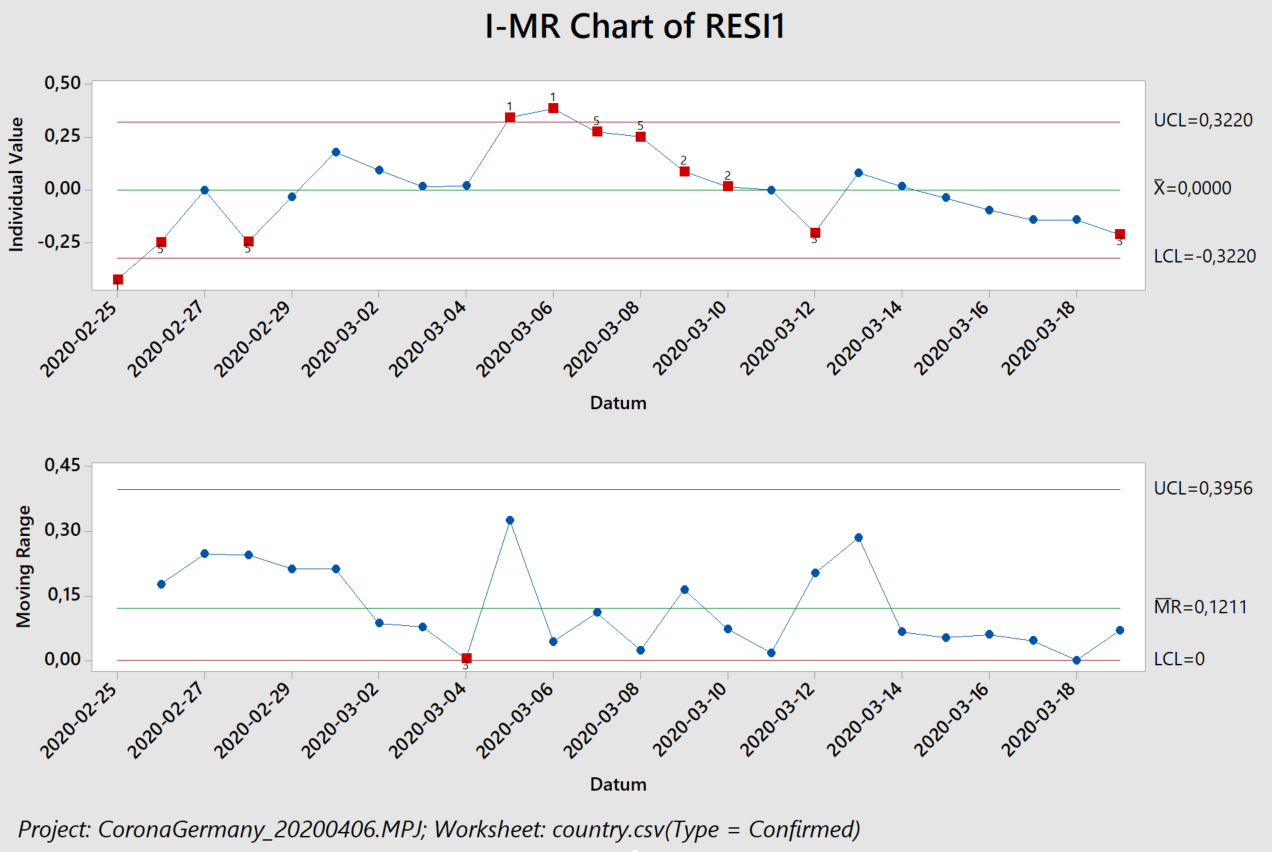
Der Algorithmus erkennt in logarithmischer Auftragung, links, zunächst einen ansteigenden Trend in den Residuen (Abstand zwischen den schwarzen Punkten und der blauen Ausgleichsgeraden). Dieser Trend führ auch zu einer eindeutigen Verschiebung („Shift“) und dann zu einem abfallenden Trend. Das exponentielle Modell beschreibt die Daten also schlecht, was wir auch an einem Regressionskoeffizienten von 92% erkennen. Rein rechnerisch erhält man zwar weiterhin eine Verdopplungszeit (von 20,5 Tagen), sollte diese jedoch nicht für Vorhersagen verwenden, da das zugrunde liegende Modell nicht angemessen ist.

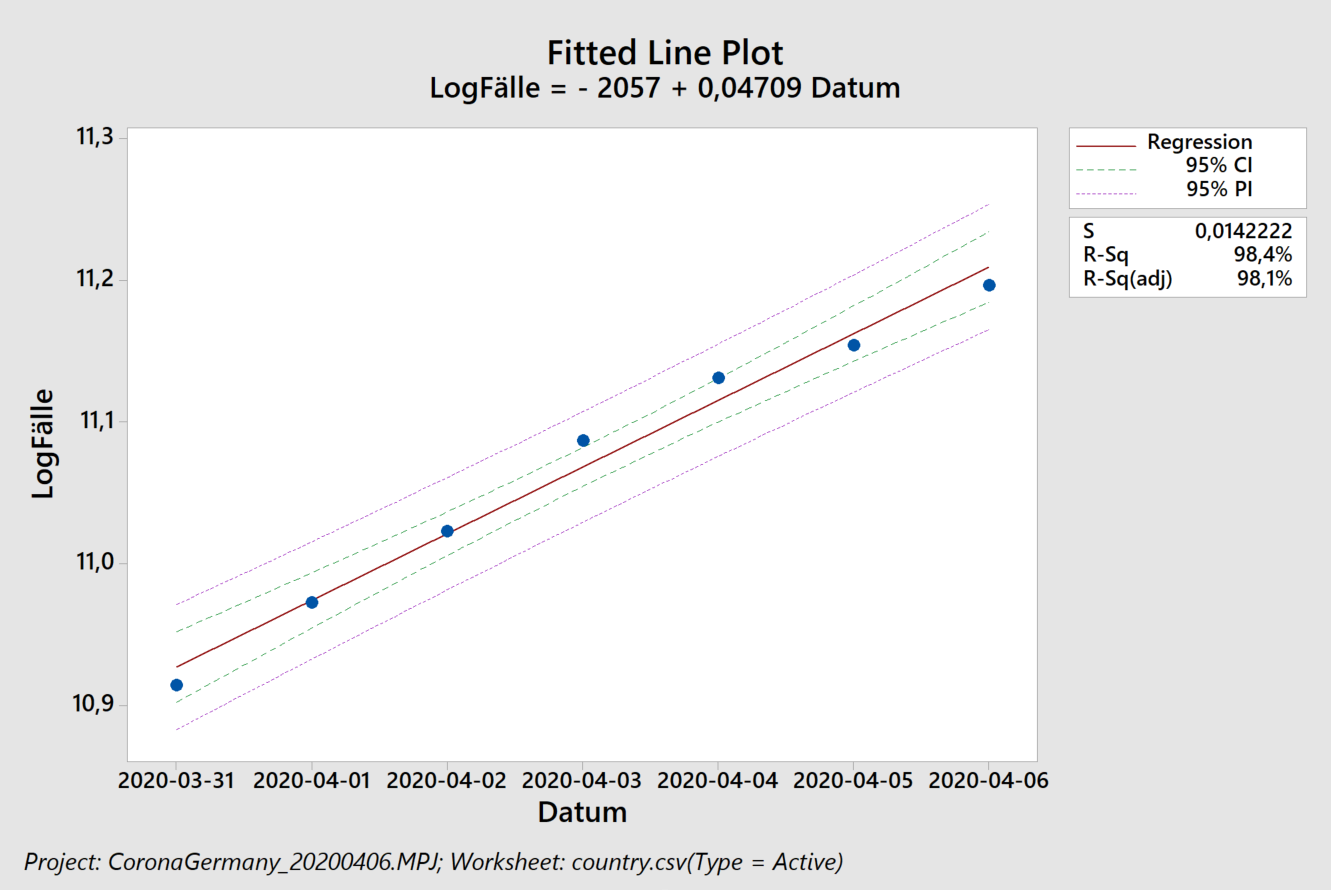
Das lineare Modell, rechts, beschreibt die Daten dagegen besser: nur drei Prozent (100% minus 97%) der beobachteten Streuung stammen nicht von dem linearen Anstieg. Wir erkennen hier jedoch auch ein ähnliches Verhalten der Residuen: selbst das lineare Wachstum ist abgebremst. Die vorhergesagten 3668 neuen Fälle pro Tag stellen also eine Abschätzung nach oben dar. Wenn wir die Zahlen lediglich ab dem 10. April herausgreifen erkennen die Western Electric / Nelson Regeln keine Besonderheiten – und wir erhalten ca. 2500 neue Fälle pro Tag (2474, um genau zu sein – wir haben im Rahmen der Fehlertoleranz gerundet).

Unter Verwendung von Littles Gesetz und einer durchschnittlichen Krankheitsdauer von 30 Tagen schätzen wir für die nähere Zukunft also einen zu erwartenden, mehr oder minder konstanten, Krankenstand von 75000 Menschen in Deutschland ab. Bei den derzeitigen Diskussionen um Lockerungen der Maßnahmen wird diese Zahl mit der Kapazität des Gesundheitssystems verglichen.

Singapur: zurück zu exponentiellem Wachstum

Werfen wir für den gleichen Zeitraum einen Blick nach Singapur:

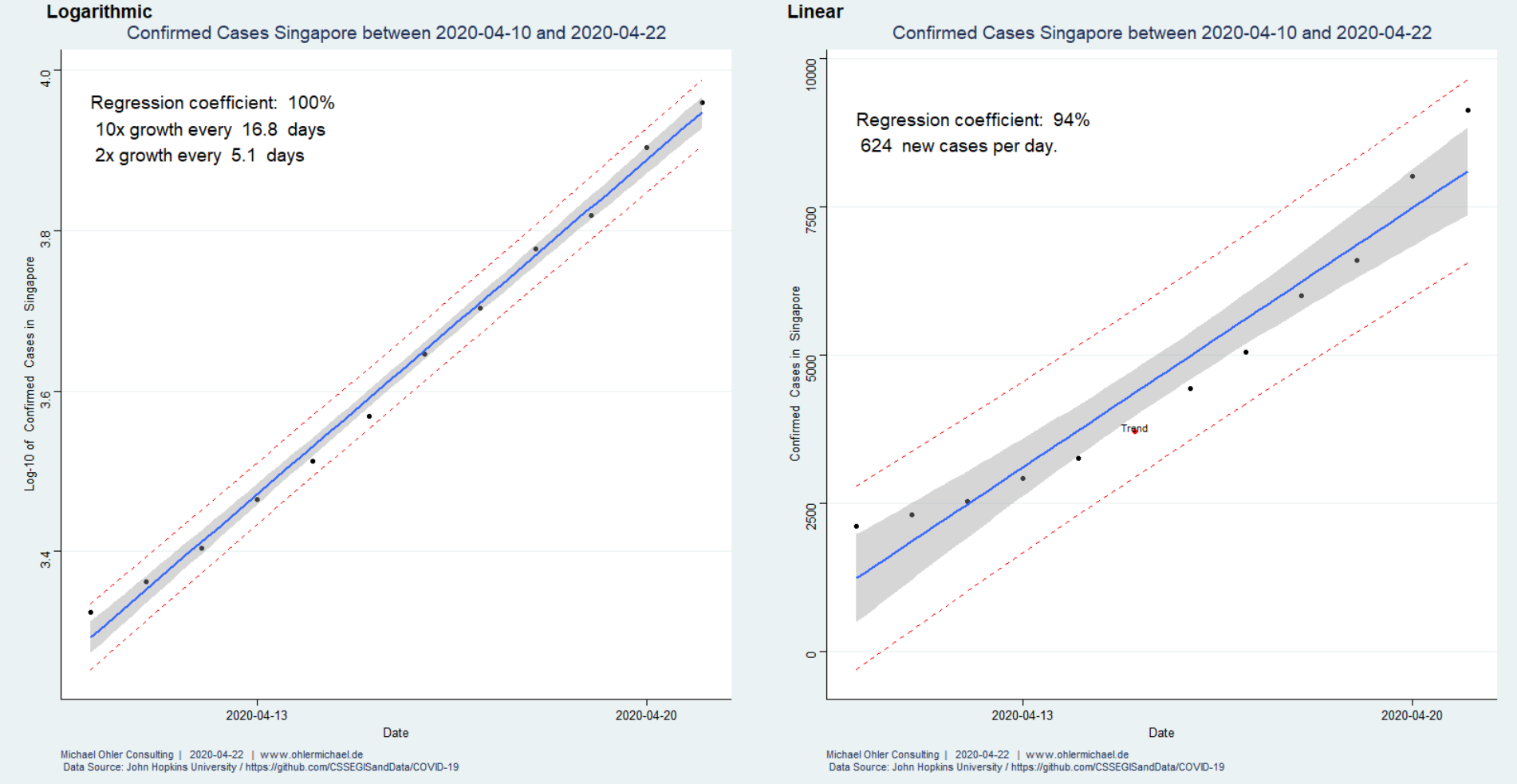
Ein lineares Wachstumsmodell (rechts) führt zu einer „Biegung“ der Residuen, die auch als Trend erkannt wird und somit signifikant ist. Das lineare Modell hat eine Güte von 94% – wohingegen ein logarithmisches Modell links die Zahlen fast perfekt beschreibt (Regressionskoeffizient nahe 100%): Singapur hat derzeit mit einer „zweiten Welle“ und einer Verdopplungszeit von 5,1 Tagen zu tun (wenn auch auf niedrigem Niveau, wie man an den 624 neuen Fällen pro Tag abliest, die das lineare Modell ermittelt). Wenn diese Welle jedoch nicht eingedämmt werden kann, dann ist im Laufe eines Monats (2*16,8) mit hundert Mal so vielen Fällen zu rechnen (Verzehnfachung der Verzehnfachung).

Automatisierte Erkennung von Infektionsherden

Auch in Deutschland wird man die Zahlen im Auge behalten müssen, um solch eine „zweite Welle“ schnell zu erkennen. Untersuchungen, die wir hier für ganze Länder durchführen, können auch regional angewendet werden und so frühzeitig warnen. Mit unserem R-Programm sind wir auch in der Lage, Länder und Regionen nicht nur schnell manuell zu betrachten – es genügt die Änderung eines Eintrages im Quellcode, was in wenigen Sekunden getan ist. Wir können auch Schleifen über mehrere Regionen und Länder durchlaufen, automatisiert modellieren und nach Verletzungen der Nelson-Regeln suchen. Man stelle sich dies vor für alle Postleitzahlen in Deutschland: Infektionsherde lassen sich so sehr schnell erkennen.

Wir sind überzeugt, dass genau dies oder ähnliches derzeit aufgebaut wird: entscheidend dafür sind nämlich gute Zahlen und es gilt, flächendeckend zu testen.

USA: lineares Wachstum mit erschreckend hoher Rate

Für die USA betrachten wir zunächst den Gesamtverlauf:

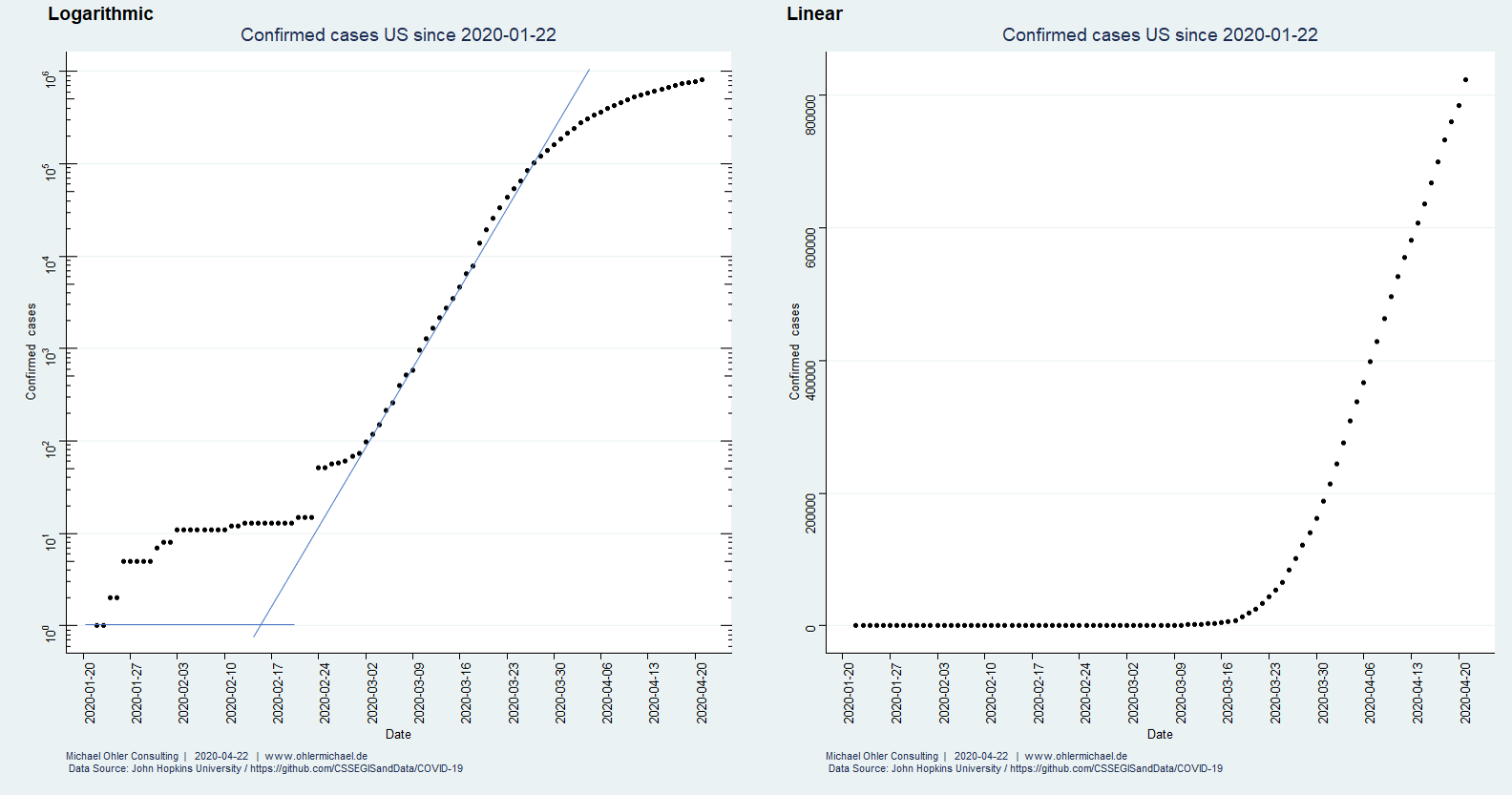
Wir erkennen deutlich den „Weckruf-Knick“ um den 24. Februar herum, ab dem Daten systematisch erfasst werden. Wenn man möchte, dann kann man in der linken, logarithmischen Darstellung das sich anschließende exponentielle Wachstum rückwärts extrapolieren, um den Zeitpunkt der Infektion des „Patienten Null“ zu bestimmen. Wir machen das freihändig (die beiden hinzugefügten Linien) und ermitteln somit den 15. Februar als Datum für den Beginn der Epidemie in den USA.

Ab ca. dem 30. März erscheint das Wachstum nahezu perfekt linear (rechts) und wir schauen uns die Entwicklung mit den nun hinreichend bekannten Statistik-Werkzeugen genauer an:

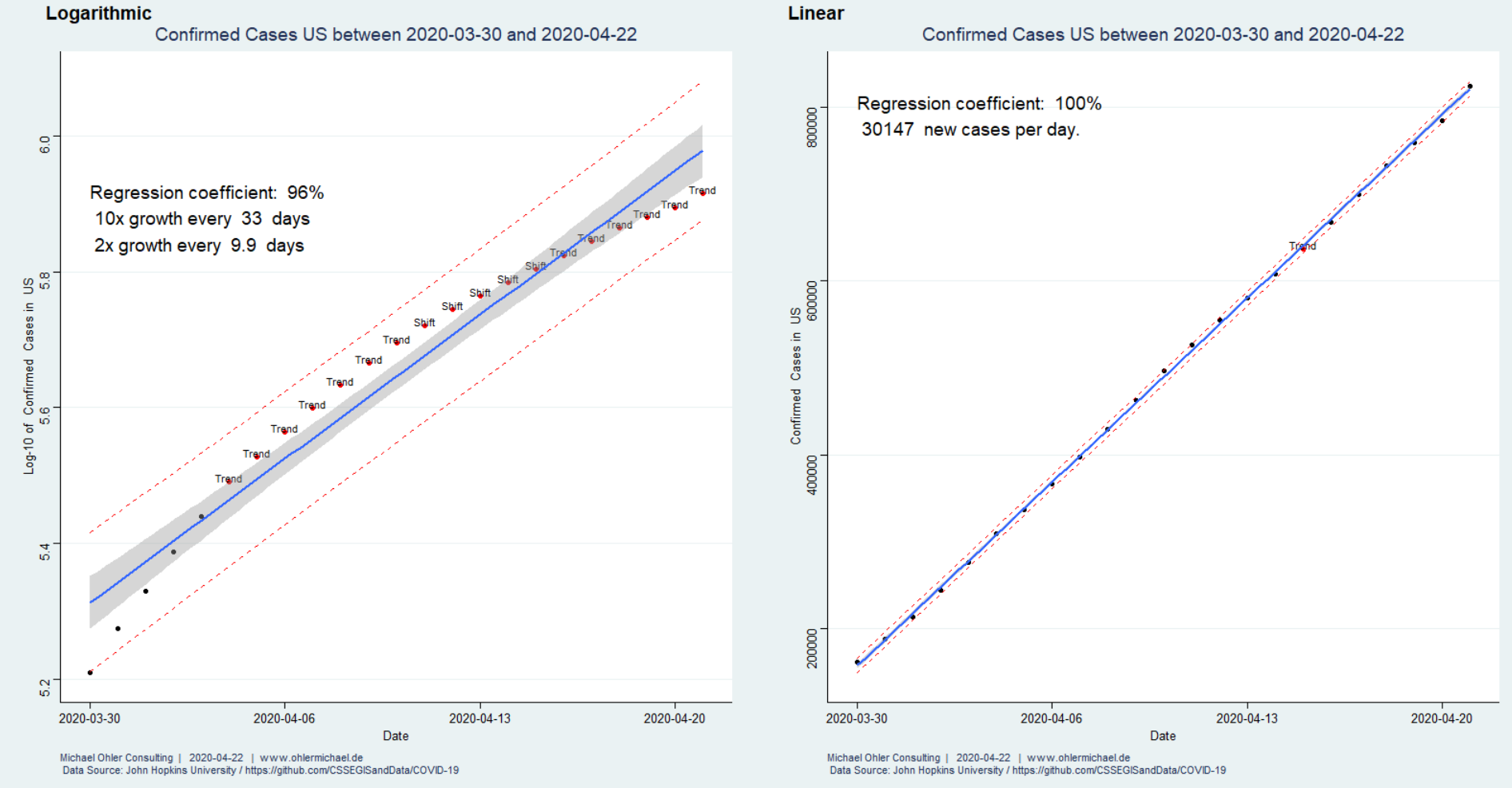
Das exponentielle Modell beschreibt das Wachstum nur unzureichend, was wir nicht nur am Regressionskoeffizienten sondern auch an dem deutlichen Trend in den Residuen erkennen. Das lineare Modell ist hingegen nahezu perfekt. Wir rechnen vorerst weiterhin mit 30000 neuen bestätigten Fällen pro Tag – die Auswirkungen auf das Gesundheitswesen, das Land und die Menschen sind für mich nicht vorstellbar.

Seit dem 22. März gilt in Deutschland ein „umfassendes Kontaktverbot“, das unserer Wirtschaft und Gesellschaft hohe Opfer abverlangt. Was hat das bisher gebracht?

Ich folge inzwischen der deutschen Presse und verwende auch die Daten der John Hopkins Universität. Etwas unscheinbar befindet sich unter der „Corona Map“ ein Link auf Github, von wo sich csv-Dateien für die bestätigten und die Todesfälle sowie die Anzahl der Genesenen herunterladen lassen. Aus diesen Zahlen berechnen wir auch die Zahl der „Aktiven“, also den Krankenstand.  

Abschätzung des zu erwartenden Krankenstandes

In logarithmischer Auftragung erkennt man eine deutliche Abschwächung der Wachstumsrate für die bestätigten („confirmed“) Fälle. Zumindest genauso wichtig ist die damit einhergehende geringere Wachstumsrate (aber weiterhin steigende Anzahl) der Kranken, die auf ein gut funktionierendes und nicht überlastetes Gesundheitswesen angewiesen sind. Am 6. April sind das mehr als 72000 Menschen. Die Entwicklung der letzten Tage tragen wir logarithmisch auf:

Das zu erwartende Wachstum des Krankenstandes über die nächsten Tage lässt sich mit dieser Regressionsanalyse abschätzen. In logarithmischer Auftragung ergibt sich wie gezeigt eine Gerade mit der Steigung 0,04709. Wir erwarten also eine Verdopplung alle 14 Tage – bei aktuellem Maßnahmenkatalog. Über das lila gezeigte Vorhersageintervall erkennen wir, dass auf Grundlage dieser auf sieben Tagen basierenden Analyse eine Vorhersage für 14 Tage mit einer erheblichen Unsicherheit behaftet ist – sowohl nach oben als auch nach unten. Da aber auch die Einführung der Maßnahmen erst 15 Tage zurückliegt, können wir vermutlich nicht von einem „stabilen System“ ausgehen. Auch deshalb werden die aktuellen Zahlen in Nachrichten und Zeitungen stets neu bewertet.

Es liegen, wenn auch nicht mir, inzwischen genügend Zahlen vor, um aus der Anzahl der „Aktiven“ abschätzen zu können, wie viele Menschen eine Intensivbehandlung benötigen. Diese Zahl lässt sich wiederum mit der verfügbaren Kapazität an Bettenplätzen, Beatmungsgeräte, usw. vergleichen. So ließe sich überlegen, inwiefern Lockerungen der Maßnahmen riskiert werden können.

Hervorgehoben werden muss, dass es sich hier um eine grobe ABSCHÄTZUNG – und zwar hoffentlich nach oben – der zu erwartenden Belastung des Gesundheitssystems handelt: modellieren sollte man besser die Ausbreitung des Corona-Virus. Über Daten von Einzelfällen mit den Zeitpunkten für Diagnose und Ausgang der jeweiligen Erkrankung, Zahlen, die verständlicherweise nicht veröffentlicht werden, lässt sich eine mittlere Krankenzeit und deren Streuung berechnen. So könnte der zu erwartende Krankenstand besser abgeschätzt werden. Wir haben diese Möglichkeit hier nicht und modellieren deshalb den Krankenstand direkt.

Was hat die „soziale Distanzierung“ gebracht?

Schauen wir uns dafür die Zahlen der Ausbreitung genauer an und hier zunächst den Anstieg zu Beginn der Epidemie in Deutschland. Über eine Analyse der Residuen (s.u.) wählen wir den Zeitraum vom 25. Februar bis zum 19. März aus. Praktisch gesprochen: während dieser Zeit konnte sich das Virus nahezu ungebremst ausbreiten und wir wollen die Geschwindigkeit bestimmen.

Die Steigung der Kurve beträgt 0,2866 – was einer Verdopplung der Fälle alle 2,4 Tage entspricht – eine Rate, die wir auch bei vielen anderen Ländern zu Beginn der Epidemie antreffen. An den Vorhersageintervallen erkennt man zudem, dass einige Punkte „verdächtig weit“ von der braun-rot dargestellten Ausgleichsgeraden entfernt liegen. Wir schauen uns den zeitlichen Verlauf dieser „Residuen“, also der Abstände von der Ausgleichsgeraden, mit einer Regelkarte genauer an:

Die „Western Electric Regeln“ oder auch „Nelson Regeln“ im medizinischen Bereich, schlagen tatsächlich Alarm und wir haben zunächst einen signifikanten Anstieg – und zwar um sechs Standardabweichungen. Genaueres führt hier zu weit, lässt sich jedoch über eine Internetrecherche nachschlagen. Wichtig ist: in den Daten steckt noch ein Signal, das in dem obigen Regressionsmodell nicht erfasst wurde, und die Ergebnisse sind deshalb mit einer gewissen Vorsicht zu betrachten.

Eine Verdopplung der insgesamt bestätigten Fälle (also nicht der täglich neuen Fälle) alle 2,4 Tage ist und bleibt allerdings dramatisch und ließ sich – in logarithmischer Auftragung – schon sehr früh erkennen. Wir haben darüber geschrieben.

Dank der inzwischen eingeleiteten Maßnahmen hat sich die Lage seither sehr zum Besseren gewendet. Aus der Steigung von 0,07132 erhalten wir eine Verdopplung alle 9,7 Tage – was immer noch schlimm genug ist:

Schauen wir uns auch hier die Residuen an:

Wenn man optimistisch ist, dann sinkt ab dem 3. April die Wachstumsrate noch weiter. Aus diesen vier Punkten erhalten wir eine Verdopplungszeit von 16,5 Tagen – bei sehr breiten Vorhersageintervallen. Es gilt also, diese Zahlen täglich zu verfolgen: sind wir eher mit einer Verdopplung alle 10 oder alle 16 Tage unterwegs? Und was bedeutet das für die Aus- und Überlastung unseres Gesundheitssystems?

Wir kommen also von einer Verdopplung alle 2,4 Tage und haben es dank der eingeleiteten Maßnahmen geschafft, die Ausbreitungsgeschwindigkeit auf eine Verdopplungszeit von bis zu 9 oder sogar mehr Tagen zu bremsen.

Können die Maßnahmen inzwischen gelockert werden?

Das ist die Frage aller Fragen, auf die es keine statistische Antwort gibt. Untersuchungen wie diese hier können leider nur helfen, die Wirkung im Nachhinein zu bewerten. Eine Aufrechterhaltung der bestehenden Einschränkungen oder eine sehr vorsichtige Lockerung muss auf jeden Fall gut kommuniziert werden. Die rapide Ausbreitung von Corona war schon früh erkennbar – die notwendigen Maßnahmen in Deutschland aber offensichtlich damals noch nicht vermittelbar. Um so massive Änderungen des öffentlichen Lebens einzuleiten, bedurfte es eines geteilten Verständnisses der Dringlichkeit – und ganz offensichtlich hat Mathematik alleine dafür nicht gereicht. Gleiches gilt für eine Aufrechterhaltung oder nur zögerliche Lockerung der aktuellen Situation.

Schauen wir uns die Zahlen von Singapur an, um zu verstehen, wie es weitergehen könnte.

Zwischen dem 22. Januar und dem 2. Februar steigen hier die bestätigten Fälle mit einer Verdopplungszeit von 2,7 Tagen an. Ab dem 15. Februar (hervorgehoben) flacht die Kurve dank der eingeleiteten Maßnahmen ab und bleibt bis zum 5. März bei einer Verdopplungszeit von 30 Tagen, die sich danach aber relativ stabil auf 8,4 Tage verkürzt.

Hat Singapur vor dem 5. März gewisse Maßnahmen gelockert? „Steuert“ der Stadtstaat seine Reglementierungen anhand von solchen Analysen? Richten sie sich dabei aus an der Kapazität des Gesundheitssystems, sodass also alle Notfälle auch entsprechend behandelt werden können? Ich weiß es nicht. Ein Anruf in Singapur könnte aber auch hierzulande für interessante Einsichten sorgen, wenn es darum geht, in wie weit und wann die derzeitigen Einschränkungen gelockert werden können.