Die Frage mag zunächst ungewöhnlich erscheinen: Wieso sollte der Planet Erde „atmen“?
Aus dem Biologieunterricht ist Dir vermutlich noch in Erinnerung, dass Pflanzen über den Prozess der Photosynthese dazu in der Lage sind, CO2 aus der Luft zu binden und Sauerstoff „auszuatmen“. Im Winter werfen Bäume ihre Blätter ab und gönnen sich eine Auszeit. Die Photosynthese kommt zum Erliegen, die heruntergefallenen Blätter verrotten und setzen dadurch CO2 frei, das im Laufe des Frühlings und Sommers wieder aufgenommen wird.
Warum Du diesen Beitrag lesen solltest
Es ist eine weithin bekannte Tatsache, dass die CO2-Konzentration in der Erdatmosphäre kontinuierlich steigt. Neben einigen anderen „Klima-Gasen“ sorgt Kohlendioxid für den „Treibhauseffekt“ unseres Planeten und trägt somit entscheidend zur Klimaerwärmung bei. Weniger bekannt ist, dass neben diesem Trend eine jährliche Oszillation zu beobachten ist. Mit öffentlich verfügbaren Daten kannst Du diese sichtbar machen und in Beziehung zum ansteigenden Trend setzen. – Wer hätte das gedacht?
Unsere heutige Fragestellung
Ein Blick auf die Weltkarte zeigt zudem, dass die Landmasse der Nordhalbkugel deutlich größer ist als die der Südhalbkugel. Der vorherigen Überlegung folgend sollte deshalb im nördlichen Winterhalbjahr die weltweite CO2-Konzentration steigen und im Sommerhalbjahr wieder sinken – der Planet „atmet“. Wenn das System Erde im Gleichgewicht wäre, dann würde die CO2-Konzentration der Atmosphäre um einen gewissen Mittelwert herum im Rhythmus der Jahreszeiten schwanken.
Wir stellen uns deshalb heute folgende Fragen:
Wie tief ist dieser „Atemzug“ des Planeten Erde? Und wie groß sind im Vergleich dazu der mittlere Anstieg der CO2-Konzentration in der Atmosphäre und die menschengemachten CO2-Emissionen?
Wir wollen uns dieser Frage mittels „OSAN“ (englisch: Open Source ANalytics) zuwenden, also öffentlich zugängliche Daten nutzen. Den Begriff scheint es bisher nicht zu geben. Wohl aber wird von „OSINT“ gesprochen (Open Source INTelligene) und so bietet sich OSAN als Beschreibung dessen an, was wir hier betreiben.
Wie wir vorgehen wollen
Wir verwenden die Skript-, Berichts- und Webapplikationssprache R, die speziell für die Handhabung von Daten, Texten und zunehmend auch Bildern entwickelt wurde. Du kannst Sie kostenfrei installieren und hast so auf einen Schlag Zugang zu den neuesten und besten Analysewerkzeugen. Der Vorteil unserer Herangehensweise hier liegt vor allem auch darin, dass Du Deine Analysen ständig aktuell halten kannst: einmal „Run“ gedrückt und schon lädt Dein Skript wieder die neuesten Daten herunter und wertet sie für Dich aus.
Woher unsere Daten kommen
Seit März 1958 misst das Mauna Loa Observatorium auf Hawaii Woche für Woche die CO2-Konzentration der Erdatmosphäre. Damals hat noch niemand vom Klimawandel gesprochen und es bestand vermutlich ein rein wissenschaftliches Interesse an den Messungen. Der Mauna Loa Vulkan wurde deshalb ausgewählt, weil er weit ab von Industriezentren liegt und so eine möglichst unverfälschte Messung erlaubt.
Wir beschaffen die Daten mit den folgenden Zeilen Skript. Eine gewisse Schwierigkeit stellen die Kommentarzeilen in dem Dokument dar. Möglicherweise ändert sich deren Anzahl im Laufe der Zeit – heute sind es 44 Zeilen. Dann musst Du Dir die Daten über den Link anschauen und die skip-Option der read.csv()-Funktion entsprechend anpassen:
# Paket für Handhabung der Daten:
library(tidyverse)
# Datenquelle:
link <- "https://scrippsco2.ucsd.edu/assets/data/
atmospheric/stations/in_situ_co2/weekly/
weekly_in_situ_co2_mlo.csv"
# Daten herunterladen:
MaunaLoa <- read.csv(link,
header = FALSE,
skip = 44,
comment.char = "\"")
# Daten formatieren:
colnames(MaunaLoa) <- c("Week", "Conc")
MaunaLoa$Week <- as.Date(as.character(MaunaLoa$Week),
format = "%Y-%m-%d")
# Graphische Darstellung:
ggplot(data = zeitraum) +
geom_point(mapping = aes(x = Week,
y = Conc))
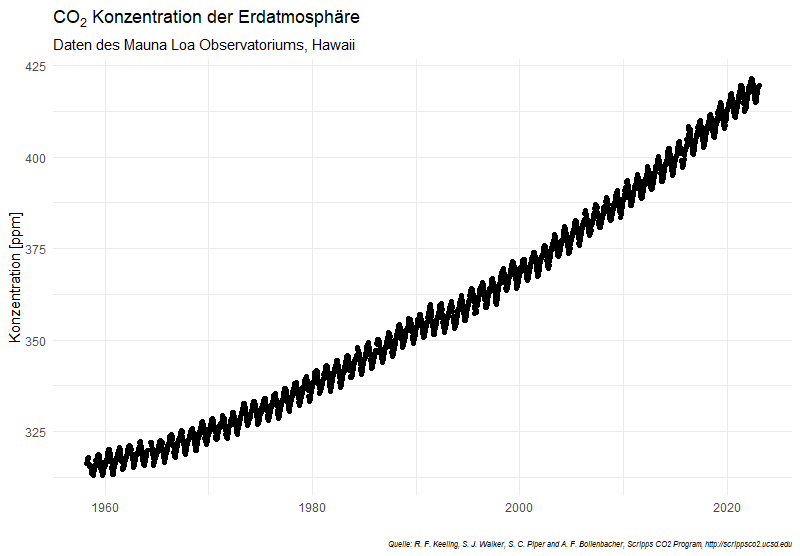
Graphische Darstellung der CO2-Daten des Mauna Loa Observatoriums auf Hawaii: Anstieg der CO2-Konzentration und jährliche Schwankungen. Dargestellt ist die Konzentration in „ppm“ (parts per million), also die Anzahl CO2-Moleküle je eine Millionen Moleküle Luft.
Trennung von jahreszeitlichen Schwankungen und langfristigem Trend
Wir sehen, was wir erwartet haben:
Die CO2-Konzentration in der Erdatmosphäre steigt beständig an. Sie durchläuft zudem jährliche Schwankungen.
Bei genauerem Hinsehen erkennst Du einige Besonderheiten: so scheint sich in den frühen 1990er Jahren ein kurzes „Plateau“ gebildet zu haben. Die Gründe dafür werden Experten längst bekannt sein. Wir wollen der Einfachheit halber die Daten ab 1995 verwenden, um Anstieg und Jahresschwankungen besser zu verstehen. Zudem fügen wir noch eine weitere Spalte an („mutate“), in der wir die Tage seit dem ersten Eintrag ablegen:
zeitraum <- MaunaLoa %>%
filter(Week >= "1995-01-01") %>%
mutate(Days = difftime(Week,
zeitraum$Week[1],
units = "days") %>%
as.numeric())
Heute möchte ich die Daten mit einem Polynom modellieren. Die Hintergründe zu dem Vorgehen hat die FU Berlin ins Netz gestellt. So können wir den langfristigen Trend erfassen. Durch „Spielen“ mit der Ordnung des Polynoms sehen wir auch, dass eine zweite Ordnung ausreichend ist und höhere Ordnungen nicht mehr signifikant sind. Wir interessieren uns zudem für die Zusammenfassung des Modells und die dazugehörigen 95%-Vertrauensintervalle der Parameter. Die Details erspare ich Dir hier. Mit den folgenden Code-Zeilen kannst Du sie Dir leicht selbst beschaffen:
# Modell erstellen:
model <- lm(Conc ~ poly(Days, 2, raw = TRUE),
data = zeitraum)
# Güte des Modells und der Parameter:
summary(model)
confint(model, level = 0.95)
# Modell und Residuen anzeigen:
plot(fitted(model), residuals(model))
# Trend und Schwankungen anfügen:
zeitraum$Trend <- model$fitted.values
zeitraum$Oszillation <- model$residuals
Wir erhalten so folgende Aussage (für die wir ein lineares Modell oder ein Polynom erster Ordnung rechnen):
Seit dem Jahr 1995 steigt die CO2-Konzentration der Erdatmosphäre Jahr für Jahr im Mittel um 2,1 ppm an.
Das mag nach wenig klingen. Wie wir sehen, „läppert“ sich das über die Jahre aber durchaus zusammen. Dank unserer Modellierung können wir nun auch die jahreszeitlichen Schwankungen betrachten:
ggplot(data = zeitraum) +
geom_line(aes(x = Week,
y = Oszillation))
Ich gehe hier einen Schritt weiter und berechne für alle Jahre den jeweiligen Tag im Jahr, an dem jede Messung stattgefunden hat, um so, gemittelt über 7 Kalendertage, den Mittelwert und die Streuung der Werte zu allen betrachteten Jahren zu berechnen, die ich hier mit den jeweiligen Messwerten gemeinsam darstelle:
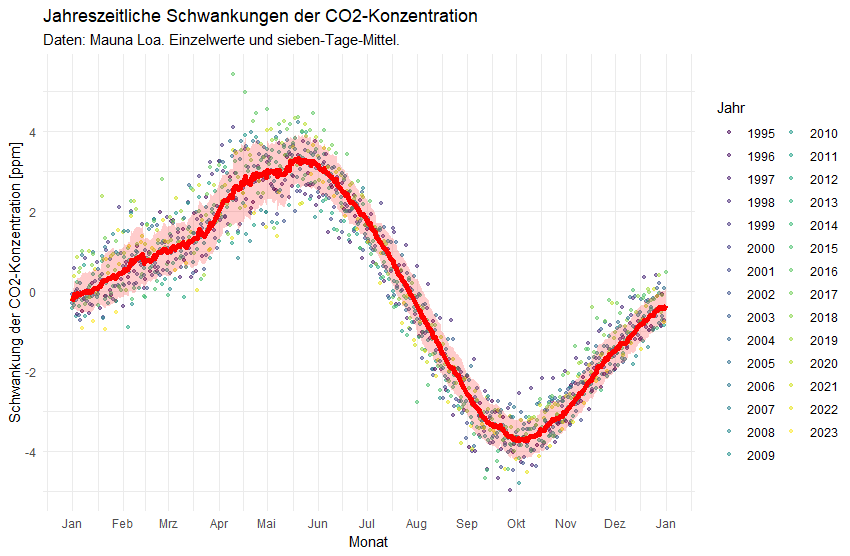
Jahreszeitliche Schwankung der CO2-Konzentration. Mittelwert (Linie) und Standardabweichung (Schlauch), zusammen mit den Einzelwerten der betrachteten Jahre.
Diese Graphik wollen wir uns auf der Zunge zergehen lassen: von Mitte Mai bis Anfang Oktober nimmt Jahr für Jahr die CO2-Konzentration der Erde um ca. 6,5 ppm ab (von ca. +3 ppm auf -3,5 ppm), um danach wieder anzusteigen. Die Erde „atmet ein“ und sie atmet wieder aus. Wir halten fest:
Die Erde hat ein Atemvolumen von ca. 6,5 ppm. Das entspricht in etwa dem mittleren Anstieg der CO2-Konzentration innerhalb von drei Jahren.
Anhand der Standardabweichung (der rosa Schlauch um den Mittelwert) erkennst Du zudem, dass der Frühlingsanfang größeren Schwankungen unterworfen zu sein scheint als der Beginn des Herbstes. Das ist interessant und wir fragen uns, ob der Frühling womöglich im Laufe der Zeit immer früher beginnt: Dafür tragen wir über die Jahre hinweg den Zeitpunkt auf, zu dem das Maximum der CO2-Oszillation erreicht wurde, stellen dabei aber kein signifikantes Signal fest. In R ist der Code dafür recht einfach (probiere das einmal in Excel…). Ich habe vorher alle Daten ab 1958 mit einem Polynom dritter Ordnung modelliert und so die Oszillationen für den gesamten Zeitraum berechnet, über die ich mir das jeweilige jährliche Maximum mittels slice_max() beschaffe. Nach einem „Signal“ suche ich mittels IMR-Regelkarte. Mit folgendem Code kannst Du diese Untersuchung selbst durchführen – auch wenn es hier nichts zu sehen gibt:
fruehling <- MaunaLoa %>%
group_by(Jahr) %>%
slice_max(Oszillation) %>%
select(Jahr, TagImJahr)
# IMR-Regelkarte
library(qcc)
imr <- qcc(fruehling$TagImJahr, type = "xbar.one")
Wie sieht es mit den menschengemachten CO2-Emissionen aus?
Dieser Frage nähern wir uns mit folgenden, vermutlich grob vereinfachenden Annahmen:
- Die auf dem Mauna Loa gemessene CO2-Konzentration ist ein gutes Maß für die mittlere CO2-Konzentration der gesamten Erdatmosphäre
- Die Masse der Erdatmosphäre ist über die Jahre hinweg konstant. Wir finden dafür auf Wikipedia den Wert von 5,15*10^18 kg.
Über diese Annahmen lässt sich die in ppm gemessene CO2-Konzentration umrechnen in die in der Atmosphäre enthaltenen Masse an CO2. Dafür verwende ich ein Molgewicht von 28,8u für Luft (80% Stickstoff mit 28u und 20% Sauerstoff mit 32u) und von 44u für CO2. Auf Statista.com finde ich zudem einen Wert für die menschengemachten jährlichen CO2-Emissionen in Höhe von 37,1 Milliarden Tonnen (im Jahr 2021). So erzeuge ich folgende Graphik. Den „langfristigen Anstieg“ habe ich dabei über ein lineares Modell berechnet:
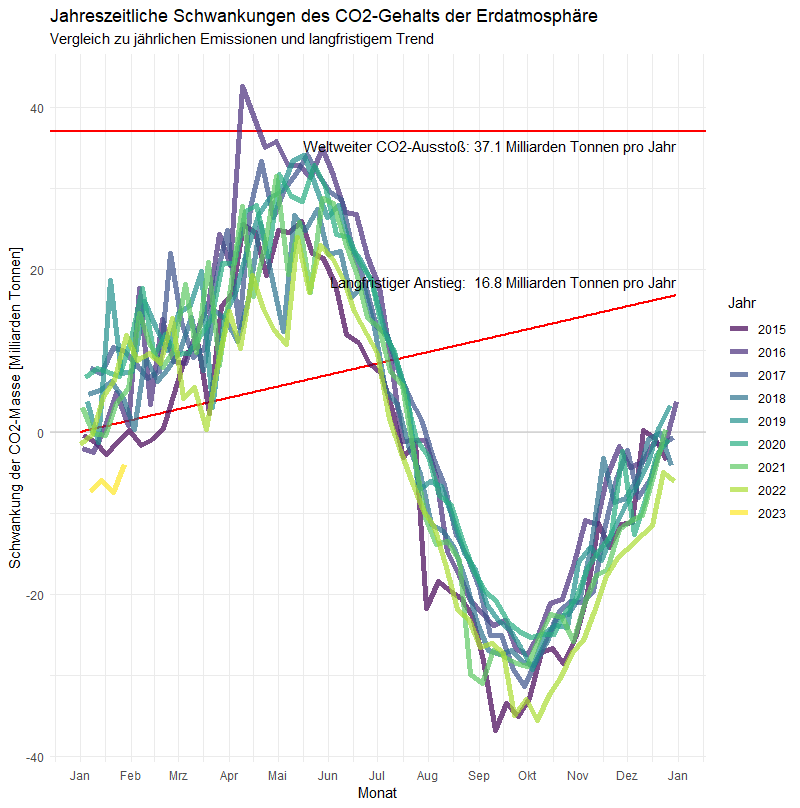
Jährliche Oszillation der CO2-Konzentration getrennt von dem überlagerten langfristigen Anstieg und im Vergleich zu den jährlichen weltweiten CO2-Emissionen.
Das Jahr 2023 fängt interessanterweise mit besonders niedrigen Werten an: es lohnt sich vermutlich, diese Entwicklung weiter im Blick behalten. Die wesentlichen Einsichten wollen wir festhalten:
Der jährliche „Atemzug“ der Erde (Maximum zu Minimum) entspricht in etwa 70 Milliarden Tonnen CO2. Das ist etwa doppelt soviel wie die Menschheit Jahr für Jahr emittiert. Jedes Jahr steigt die Masse an CO2 in der Erdatmosphäre um ca. 17 Milliarden Tonnen an.
Du wirst nun fragen:
Und wo bleibt bitteschön der Rest?
Denn die Menschheit emittiert 37 Milliarden Tonnen, von denen – unter den hier gemachten Annahmen und mit den hier verwendeten Zahlen – ca. „nur“ 17 Milliarden Tonnen in der Atmosphäre verbleiben.
Der Planet scheint einen gewissen Anteil der weltweiten Emissionen anderweitig „wegzupacken“.
In Forschung und Wissenschaft ist sicher bekannt, welche Mechanismen dafür verantwortlich sind: hoffentlich möglichst viel natürliches „Carbon Capture and Storage“ (CCS)? Mir fallen hier Muscheln und Krustentiere ein, die ihre Schale mit Kalk (CaCO2) bilden und nach Ableben im Meer zu Boden sinken. Im Laufe der Zeit kommt dabei einiges zusammen – zu besichtigen in den Kalkalpen.
Wie groß ist aber der Anteil des in Ozeanen gelösten CO2? Das würde auch zu einer größeren Versauerung der Ozeane führen. So stellen sich mir folgende Fragen:
Welche Auswirkungen hat das? Wann und unter welchen Bedingungen (beim Erreichen von Kipppunkten zum Beispiel) wird das alles wieder freigesetzt? Schlummern hier vielleicht weitere Risiken als „nur“ der Treibhauseffekt in der Atmosphäre?
Jede Antwort wirft neue Fragen auf
Wir haben öffentlich verfügbare Daten verwendet und zueinander in Beziehung gesetzt (die auf Hawaii gemessene CO2-Konzentration und die weltweiten CO2-Emissionen). Dabei haben wir einen Eindruck erhalten von den Größenordnungen und konnten die – zumindest für mich als Laien – überraschende Frage nach der „CO2-Resilienz“ des Planeten aufwerfen.
Als Abschluss unserer OSAN-Betrachtung halten uns deshalb wieder einmal an Michael Ende und den Schlusssatz vieler Episoden seiner „Unendlichen Geschichte“:
„Aber das ist eine andere Geschichte. Und die soll ein andermal erzählt werden.“
Ich danke meinem Kollegen Thomas Rietdorf vom Europäischen Six Sigma Club Deutschland für seine kritische Durchsicht dieses Beitrags.
