Warum Du diesen Beitrag lesen solltest
Aktien- und Rententipps gibt es landauf, landab. Neben einem Hauskauf ist das jahrzehntelange Besparen eines Rentenplans eine der größten finanziellen Entscheidungen, die viele Menschen treffen. Allerdings musst Du den Expertinnen und Experten vieles glauben – und findest ein bis zwei Jahrzehnte später heraus, wie es gelaufen ist. Dieser Blog hilft Dir, rechtzeitig eigene quantitative Überlegungen anzustellen. Und zwar für:
- Aktienfonds
- Einzelaktien
- Gold
- Immobilien.
Wenn Du als Angestellte oder Angestellter mit Deinem aktuellen Rentenbescheid zufrieden bist, dann: herzlichen Glückwunsch! Denn in dem Fall kannst Du „rein aus Neugierde“ weiterlesen.
Haftungsausschluss
Ich möchte hier explizit auf mein Impressum hinweisen: auch dieser Beitrag dient in erster Linie der „Vision“des Blogs. Ich möchte darstellen, welche Einsichten sich über die Analyse öffentlich verfügbarer Daten gewinnen lassen. Meine Schlussfolgerungen wurden nicht im Vier-Augen-Prinzip von Expertinnen oder Experten validiert und können deshalb keine Grundlage für konkrete Maßnahmen sein. Ich bin auch nicht als Finanzberater ausgebildet.
Die Klage über uns Deutsche ist wohlbekannt
Die Deutschen sparen zu wenig.
So heißt es.
„Wie bitte??“
Magst Du einwenden.
Mit zwei großen Fragezeichen.
Denn immerhin gehören die „schwäbische Hausfrau“ und der schwäbische Hausmann auch dazu. Und zumindest DEREN Sparsamkeit ist ja sprichwörtlich!
Gemeint mit der Klage ist: unser Geld läge unter irgendeiner Matratze. Im Sparstrumpf. Auf dem Girokonto. Eben dort, wo es nicht hinsoll. Geld müsse vielmehr „arbeiten“. Zum Beispiel in AKTIEN investiert werden. Denn das sei SOOO RENTABEL, sagen die einen. Aber auch SOO GEFÄHRLICH, erwidern die anderen: „Alles futsch – verstohsch?“ (Das ist Badisch, wo ich herkomme, nicht Schwäbisch).
Dieser Weg kann ein leichter sein
Sich darüber Gedanken zu machen ist wichtig: es geht um die Rente. Deine Rente. Wenn Du gerade ins Berufsleben eintrittst, dann solltest Du genau jetzt loslegen. Wie Du es anstellst mit Deinem Sparplan für die Rente kann am Ende ohne weiteres für doppelt- oder für halb-soviel Geld sorgen. Es lohnt sich also. Und Du wirst sehen:
Dieser Weg ist eben nicht „steinig und schwer“.
Er wird vielmehr ein überraschend leichter sein.
Um es vorwegzunehmen:
Investiere regelmäßig.
Ziehe die Sache durch.
Entnimm gleichmäßig.
Zum Schluss habe ich noch einige persönliche Tipps, falls Du auch mit Deiner Bank darüber sprechen möchtest. Und ich glaube, dass Du das tun solltest.
Drei Wege zur Glückseligkeit
Vereinfacht gesagt hast Du drei Möglichkeiten:
- Nichts tun. Das ist bequem. Es kommt vermutlich nur weniger dabei heraus.
- Vertraue dem Banker. Auch gut. Denn das ist besser als nichts zu tun.
- DIY. Do it yourself. Klingt kompliziert. Ist es aber nicht. Du wirst sehen.
Meine Überzeugung vorab:
Wenn Du selbst die Winterreifen aufziehst,
oder Terrassenplatten eigenhändig verlegst,
zumindest die Zwiebeln selbst schneidest,
dann solltest Du überlegen,
ob DIY nicht Dein Weg ist.
Zumindest für einen Teil.
Deines Geldes.
Coden ist kein Hexenwerk
Um in diesem Blog zu unseren Schlüssen zu kommen, betreiben wir „Open Source Analytics“ (OSAN) und verwenden dafür frei verfügbare Datenquellen und die Skript-, Berichts- und Webapplikationssprache R, die speziell für die Handhabung von Daten, Texten und Bildern entwickelt wurde. Du kannst Sie kostenfrei installieren. Sprachen wie R und auch Python bieten Dir viele Vorteile, zum Beispiel diese:
- Du hast auf einen Schlag Zugang zu den neuesten und besten Analysewerkzeugen inklusive Dokumentation. Du kannst Dich auch bequem von „generativer“ künstlicher Intelligenz wie ChatGPT bei der Erstellung Deines Skripts coachen lassen.
- Du kannst Deine Analysen ständig aktuell halten: Einmal „Run“ gedrückt und schon lädt Dein Skript wieder die neuesten Daten herunter und wertet sie für Dich aus.
- Als Team ist Eure Lernkurve steiler: Anders als bei „Klicksoftware“ kannst Du Dein Vorgehen, inklusive aller „Tricks und Kniffe“, in einem Skript festhalten. So könnt Ihr Euer Vorgehen leicht untereinander teilen. Versuche einmal, das was wir hier tun, in Excel nachzubauen, was möglich ist, und das Excel-Blatt dann anderen zu erklären…
- Im Vergleich zu Tabellenkalkulationsprogrammen liegt der Unterschied darin, dass Deine Algorithmen von den Daten getrennt und nicht per Formeln in die Zellen verwoben werden. So ist viel deutlicher ersichtlich und nachvollziehbar, was Du tust.
- Deshalb ist es auch viel einfacher, Fehler, die sich immer einschleichen, in Deiner – oder meiner – Analyse aufzuspüren und zu korrigieren.
Wie sonst auch kannst Du diesen Beitrag auch ohne die Code-Zeilen lesen. Die Zwischenüberschriften erlauben Dir zu springen, falls bestimmte Abschnitte Dich mehr als andere interessieren.
Das „Rendite-Dreieck“: eine wichtige Visualisierung
Wie andere Tageszeitungen auch, so hat sich der Finanzteil der FAZ offensichtlich der Mission verschrieben, das Wissen um Geldfragen zu „demokratisieren“.
So lerne ich in einem Beitrag vom 19. Mai 2023 („MSCI World besser als der DAX“) das „Renditedreieck“ (siehe unten) kennen: eine aufschlussreiche Visualisierung, die wichtige, praktische Schlüsse zulässt. In diesem FAZ-Artikel stoße ich auch auf den Satz, der den heutigen Beitrag motiviert:
„… Insofern ist es verdienstvoll, dass das Deutsche Aktieninstitut nach dem Dax, dem Euro Stoxx 50 und Einzelaktien für Mitarbeiter nun auch den MSCI World als Renditedreieck gerechnet hat, und zwar in der Variante als monatlicher Sparplan“.
Echt jetzt?
Ein ganzes Institut rechnet erst „den Dax“, vielleicht nach eine Erholungspause „den Euro Stoxx 50“ und dankenswerterweise „nun auch“ den MSCI World? Das klingt nach einer Menge Arbeit. Das DAI veröffentlicht auch tatsächlich regelmäßig Renditedreiecke. Übrigens graphisch und didaktisch sehr gut aufbereitet und zum Download verfügbar. Vielleicht wurde es dort auch erfunden? Dir ist aber vermutlich klar, was das alles im Rahmen dieses Blogs bedeutet:
Eine App muss her. Kurssymbol rein.
Klick auf „als Sparplan“ oder „als Investition“.
Rendite-Dreieck raus. Fertig.
Der Dax auf Achterbahnfahrt
Dank Yahoo Finance, des quantmod-Pakets und der getSymbols-Funktion sind zumindest die Daten schnell beschafft und für unsere Zwecke aufbereitet, hier für den Dax (^GDAXI):
# Index oder Aktie:
stock <- "^GDAXI"
# Wir wollen so weit wie möglich zurückblicken:
Horizont.Jahre <- 50
end <- Sys.Date() - 1 # gestern
start <- end - 365*Horizont.Jahre
# Daten von Yahoo Finance herunterladen und aufbereiten:
Stock <- getSymbols(stock,
from = start,
to = end,
auto.assign = FALSE) %>%
as.data.frame() %>%
rownames_to_column() %>%
drop_na() %>%
select(1, 5) %>%
rename_with(~ c("Date", "Stock"), 1:2) %>%
mutate(Date = as.Date(Date))
# Graphische Darstellung
ggplot() +
geom_point(data = Stock,
aes(x = Date, y = Stock)) +
theme_minimal() +
ylab(stock)
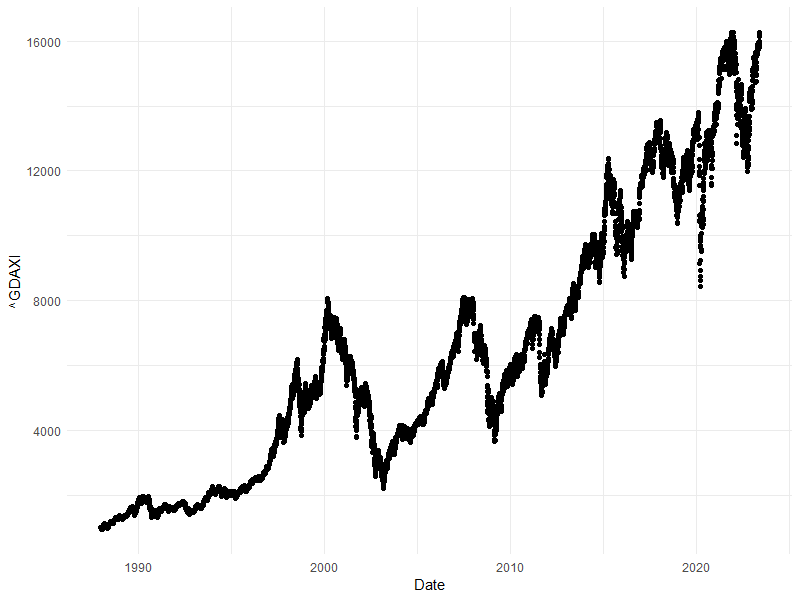
Verlauf des Dax seit dem Jahr 1987. Mit dem vorigen Code direkt aus tagesaktuellen Daten erstellt.
Was für eine Achterbahnfahrt!
Wenn Du im Jahr 2000 bei einem Kurs von 8000 eingestiegen wärst, dann hättest Du fast acht Jahre warten müssen, um Dein Geld wiederzusehen. Gleich danach wärst Du wieder „abgesoffen“ und erst im Laufe des Jahres 2014 da gelandet, wo Du im Jahr 2000 eingestiegen bist.
Angesichts solch einer Achterbahnfahrt sind Sorgen bezüglich Aktien berechtigt!
Dann allerdings, ab 2014, hätte sich Deine Anlage in den folgenden knapp 10 Jahren mehr als verdoppelt – was einer jährlichen Verzinsung von etwas mehr als 7% entspricht.
Lohnt sich das?
Oder ist das „Zockerglück“?
Darum soll es heute gehen.
Unser Zweck: die langfristige Perspektive
Es geht hier nicht um Chart-Analysen, „Unterstützungslinien“ und selbstgebastelte Aktientipps. Wir interessieren uns vielmehr für eine Perspektive von Jahrzehnten, von Deinem Einstieg ins Berufsleben bis hin zur Rente. Es geht uns auch um die Frage, ob eine Anlage in den Dax, den MSCI World, einen anderen Index-Fonds oder vielleicht auch in Gold oder Einzelaktien für die Altersvorsorge taugt. Denn wenn dem so wäre, dann könntest Du inzwischen über Direktbanken sehr günstig solche Zertifikate erwerben und halten. Die fälligen Kosten und Steuern – sowie die leidige Inflation – lasse ich aus unserer Betrachtung heraus.
Dieser Beitrag darf, kann und will Dir Deine eigene Entscheidung jedoch nicht abnehmen. Aber mit dem Renditedreieck, das Du für jeden Index, jede Aktie und auch für Gold selbst erstellen kannst, hast Du eine wichtige Entscheidungsgrundlage. Du musst nur in dem hier geteilten Code die Variable „stock“ (siehe oben im Code) anpassen.
Das Szenario „kaufen – halten – verkaufen“
Zunächst einmal möchte ich folgendes einfache Szenario betrachten: Du kaufst einen ETF (Exchange Traded Fund) zum Beispiel auf den Dax und lässt ihn einfach liegen. Wir möchten wissen, wie sich Deine Investition im Laufe der Jahre entwickelt. Das möchten wir für verschiedene Einstiegszeitpunkte betrachten und graphisch darstellen.
Auch wenn die Daten auf Tagesbasis vorliegen, betrachten wir bei diesem Anlagehorizont Jahresscheiben und bereiten die Daten entsprechend auf. Wir wählen deshalb den Kursstand zu jedem Jahresstart aus den Daten aus. Indem Du die Variable „period“ änderst, kannst Du selbstverständlich auch einen anderen Rhythmus wählen:
# In diesem Rhythmus betrachten wir die Entwicklung:
period <- "year"
# Jahresscheiben erstellen:
t <- Stock %>%
mutate(Period = floor_date(Date, period)) %>%
group_by(Period) %>%
filter(Date == min(Date)) %>%
select(Period, Stock)
# Kauf- und Verkaufstabelle erstellen.
# Dafür kreuzen (crossing) wir die Kaufs- und Verkaufstabellen,
# filtern SellDate > BuyDate
# und berechnen neue Spalten mit mutate:
t2 <- t %>%
select(Period, Stock) %>%
rename(BuyDate = Period,
BuyValue = Stock) %>%
crossing(t %>%
select(Period, Stock) %>%
rename(SellDate = Period,
SellValue = Stock)) %>%
filter(SellDate > BuyDate) %>%
mutate(HoldTime.Days = difftime(SellDate,
BuyDate,
units = "days") %>%
as.numeric()) %>%
mutate(HoldTime.Years = round(HoldTime.Days/365, 1)) %>%
mutate(Ratio = SellValue/BuyValue) %>%
mutate(Percent.per.Year = Ratio^(365/HoldTime.Days) - 1) %>%
mutate(Percentage = paste(round(Percent.per.Year*100, 0),
"%", sep = "")) %>%
mutate(Intervals = cut(Percent.per.Year,
breaks = my_breaks,
labels = my_labels)) %>%
mutate(Intervals = factor(Intervals, levels = my_labels))
In dieser Tabelle t2 liegen nun alle Daten vor. Das Weitere ist ausschließlich der Visualisierung gewidmet – wie auch schon die letzten drei mutate-Anweisungen.
Erstellung des Renditedreiecks
Ich möchte, dass das Renditedreieck für verschiedene Aktien und Indizes jeweils die gleichen Farbskala aufweist. So lässt sich der MSCI World leichter mit dem Dax, dem Euro Stoxx 50 und auch mit Einzelwerten vergleichen. Diese Anforderung macht meinen Code etwas komplizierter. Deshalb habe ich in den obigen Zeilen die Renditewerte („Percent.per.Year“) mit „my_breaks“ in Intervalle aufgeteilt, diese mit „my_labels“ beschriftet und zudem eine eigene Farbtabelle erstellt. Breaks, Labels und Farbtabelle kannst Du selbstverständlich anpassen:
# So erstellen wir die Farb-Umbrüche:
my_breaks <- c(-Inf, -0.5, -0.4, -0.3, -0.2, -0.1, -0.05, -0.03, -0.01,
0.01, 0.03, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, Inf)
my_labels <- c("<-50%", "-50%..-40%", "-40%..-30%", "-30%..-20%",
"-20%..-10%", "-10%..-5%", "-5%..-0.3%", "-3%..-1%",
"-1% .. 1%", "1%..3%", "3%..5%", "5%..10%", "10%..20%",
"20%..30%", "30%..40%", "40%..50%", ">50%")
# Farbcodes:
color1 <- "#8B0000" # dark red
color2 <- "#FFFFFF" # white
color3 <- "#006400" # dark green
colourtable <- data.frame(
Intervals = my_labels,
colours = colorRampPalette(colors = c(color1, color2, color3))(17)
)
Die Schwierigkeit besteht nun darin, dass nicht jedes Renditedreieck alle Intervalle ausgeschöpft. Deshalb untersuche ich zunächst, welche aktuellen Farben („current_colours“ im nächsten Code-Block) vorliegen und verwende diese für die Einfärbung der Kacheln (tiles) in ggplot. Falls Du lieber Quartals- als Jahresscheiben betrachtest, was Du oben über die Variable „period“ einstellen kannst, dann lasse ich Dir die Fallunterscheidung noch im Code, sodass auch die Prozentwert-Beschriftungen in den Kacheln in einer passenden Größe erscheinen. Die vielen Formatanweisungen des ggplot lasse ich ebenfalls stehen – auf die Gefahr hin, dass es abschreckend wird. Aber so kannst Du den Code übernehmen und gleich loslegen:
# Wir berechnen die Farben DES VORLIEGENDEN Graphen,
# in der richtigen Reihenfolge:
current_colours <- t2 %>%
arrange(Percent.per.Year) %>%
select(Intervals) %>%
unique() %>%
left_join(colourtable)
# Textgröße für Beschriftung der Zellen im Dreieck:
text.size <- case_when(
period == "year" ~ 3,
period == "quarter" ~1)
p <- ggplot(data = t2,
aes(x = SellDate,
y = BuyDate,
fill = Intervals)) +
geom_tile() +
scale_fill_manual(values = current_colours$colours) +
labs(title = paste("Renditedreieck", stock, sep = " "),
x = "Verkauf",
y = "Kauf") +
# Ab hier folgen Formatanweisungen für die Darstellung:
theme_minimal() +
theme(panel.background = element_rect(fill = "white")) +
scale_y_date(date_labels = "%Y",
date_breaks = "5 years",
date_minor_breaks = "1 year") +
scale_x_date(date_labels = "%Y",
date_breaks = "5 years",
date_minor_breaks = "1 year") +
geom_text(aes(label=paste(round(Percent.per.Year*100),
"%", sep = "")),
color="black",
size = text.size) +
guides(fill = guide_legend(title = NULL)) +
theme(legend.position = c(0, 1),
legend.direction = "horizontal",
legend.justification = c(0,1))
p
# Falls Du die Graphik abspeichern möchtest:
ggsave(filename = "MeinErstesrenditeDreieck.png",
width = 20, height = 10, dpi = 300)
So erhalten wir nun endlich das Renditedreieck:
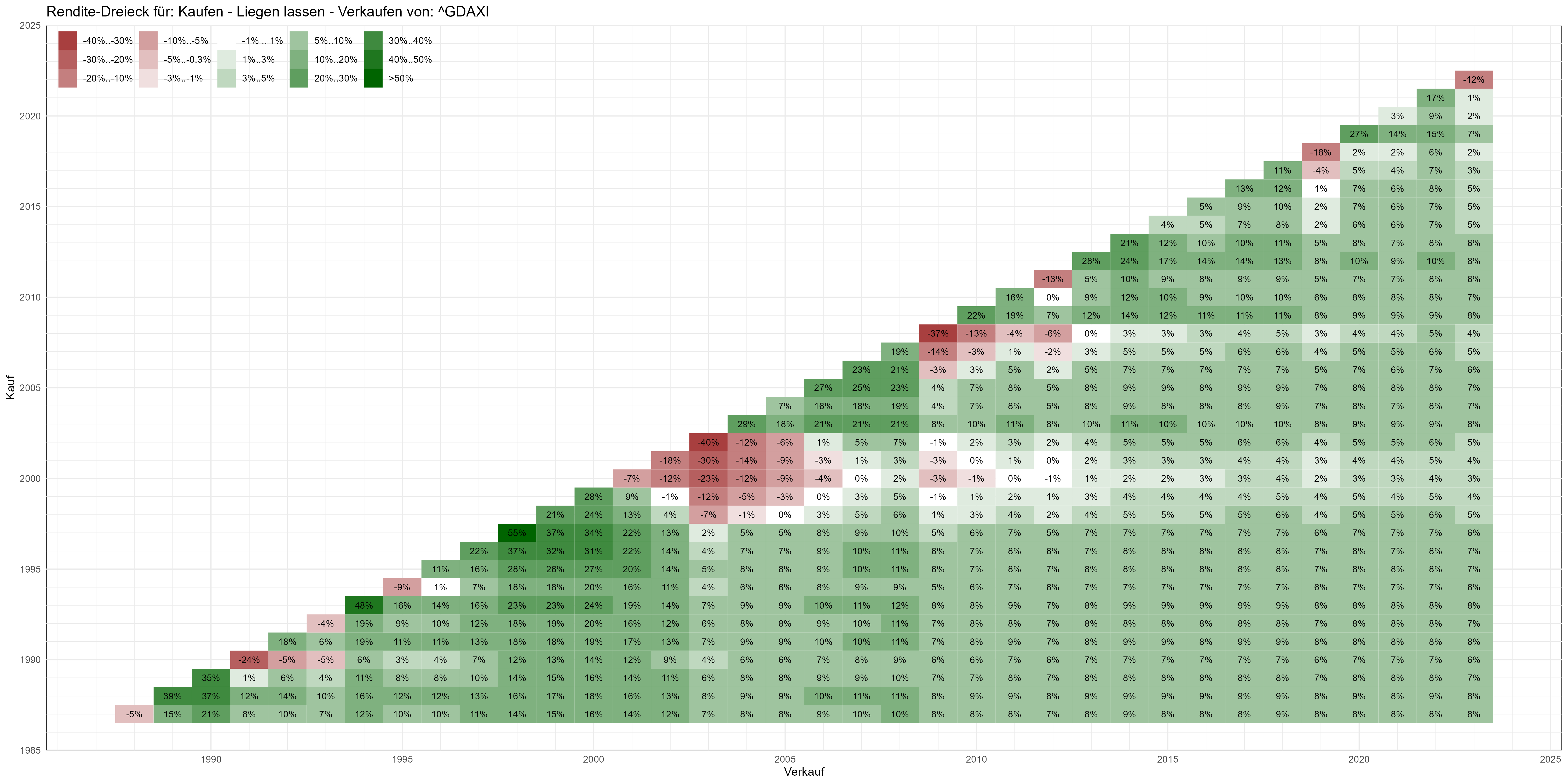
Renditedreieck des Dax für das Szenario: Kaufen – Liegen lassen – Verkaufen. Im Jahresrhythmus gerechnet. Vertikale Achse: Jahr des Kaufs. Horizontale Achse: Jahr des Verkaufs. In den Zellen abgebildet ist die jeweilige jährliche Rendite der Investition, Jahr für Jahr. Ohne Gebühren und Steuern gerechnet. Je nach dem, welchen Bildschirm Du verwendest, musst Du das Bild vergrößern, um alles lesen zu können. Du kannst es auch abspeichern (dafür mit der rechten Maustaste darauf klicken).
Wie Du das Renditedreieck liest
Auf der vertikalen Achse ist das Jahr des Kaufs dargestellt, auf der horizontalen das des Verkaufs. Es ergibt sich ein aufsteigendes Treppchen, weil man natürlich nicht früher verkaufen als kaufen kann. In den Kacheln dargestellt ist die jeweils erzielte Rendite der Anlage. Für jedes Verkaufsjahr entspricht die oberste Kachel, die „Stufe“ also, einer Haltezeit von einem Jahr. Bei einem gegebenen Einkaufsjahr gehst Du für längere Haltezeiten horizontal in das Dreieck hinein. Rote Kacheln entsprechen Verlusten, grüne Kacheln entsprechen Gewinnen und bei weißlich gefärbten wärst Du mehr oder weniger bei Null herausgekommen.
Schauen wir uns ein Beispiel an.
Wenn Du am 1. Januar 2002 in den Dax eingestiegen (vertikale Achse) und am 1. Januar 2003 schon wieder ausgestiegen wärst (horizontale Achse), was einer Haltezeit von einem Jahr entspricht, dann hättest Du satte 40% verloren. Allerdings hätte es sich gelohnt, die Nerven zu bewahren: bei einem Ausstieg schon im Folgejahr (eine Kachel weiter in horizontaler Richtung) hätten sich Deine Verluste auf 12% p.a. und bei einem Verkauf zum 1. Januar 2005 auf 6% p.a. begrenzt. Ab dem Jahr 2014 (bei gleicher vertikaler Position gehen wir auf der horizontalen Achse auf dieses Jahr) hättest Du aus Deiner Investition sogar eine jährliche Rendite von 5% herausgeholt. Bei einer Anlage von 1000 Euro im Jahr 2002 wären bis Anfang 2023 also 2790 Euro zusammengekommen, also mehr als doppelt soviel.
Ist das Zockerglück?
Für diese Frage schauen wir uns das Rendite-Dreieck genauer an: parallel zur Hypotenuse verlaufen die Linien gleichen Investitionshorizonts. Je größer der Abstand einer roten Kachel von der Hypotenuse desto länger hättest Du für diese Investition auf Dein Geld warten müssen. Über den gesamten Zeitraum betrachtet wäre eine Investition am 1. Januar 2000 die schlechteste gewesen, denn Du hättest selbst im Jahr 2010 noch ein Minus von einem Prozent pro Jahr gemacht. Das nächst-schlechte Einstiegsjahr wäre 2007 gewesen: bei einem Verkauf im Jahr 2012 hättest Du 2% Verluste pro Jahr eingefahren. Aber danach geht es nach oben.
Ist das „Zocken“?
Oder zahlt sich letztlich Geduld aus?
Wenn Du auf den Dax setzt, dann schließt Du eine Wette darauf ab, dass es mit der deutschen Wirtschaft, zumindest langfristig, „schon irgendwie bergauf gehen wird“. Im Betrachtungszeitraum heißt „langfristig“, dass Du einen Horizont von mehr als 10 Jahren mitbringen solltest, um auf der sicheren Seite zu liegen. Bei Berufseinstieg bringst Du etwa 40 Jahre mit.
Dax, Dow Jones oder MSCI World?
Eine andere spannende Frage ist natürlich: Soll ich wirklich in den Dax investieren? Oder lieber auf den Dow Jones setzen, einen MSCI-World-ETF kaufen oder doch in Einzelaktien gehen?
Solche Fragen beantwortet Dir Deine Bank sicher gerne – und empfiehlt Dir vielleicht stattdessen auch ein paar gemanagte Fonds – mit Ausgabeaufschlägen und Verwaltungsgebühren. Das kann durchaus eine sinnvolle Ergänzung oder Alternative sein. Dazu unten einige persönliche Gedanken.
Mein Vorschlag ist: baue das oben dargestellte Skript nach und passe die Variable „stock“ für den Index oder die Aktie an, die Dich interessieren. Und rechne auch einmal das Renditedreieck für den Nikkei. Du erinnerst Dich vielleicht: der hatte im Jahr 1990 seinen Höchststand…
Das Renditedreieck für den kontinuierlichen Sparplan
Unser bisheriges Szenario ist natürlich unrealistisch: Rentenpläne werden in der Regel kontinuierlich bespart. So könntest Du zum Beispiel beschließen, Monat für Monat 100 Euro zurückzulegen. Schön wäre es, wenn Du dabei nicht nachdenken müsstest: „Soll ich diesen Monat besser nicht, oder vielleicht ‚jetzt erst recht‘ kaufen?“
Ohne solche Gedanken hättest Du weniger Kopfschmerzen: Wenn alle von „Krise“ sprechen, dann machst Du genauso weiter wie zu Zeiten größter Euphorie. So wirst Du manchmal teuer einkaufen (zu „Bullenmarkt“-Zeiten, wenn alle sagen, dass Du kaufen sollst), manchmal günstig (in einer „Bärenmarkt“-Stimmung, wenn alle Dir davon abraten). Interessant wäre also, wie das Renditedreieck für dieses Szenario aussähe – und das hat ja schließlich auch das Deutsche Aktieninstitut gerechnet.
Wir stellen wir uns deshalb die Frage: welche Rendite, Jahr für Jahr, erhalten wir für solch eine kontinuierliche Investition? Um das zu rechnen, betrachten wir die Zahlungsströme: Monat für Monat gehen von Deinem Konto zum Beispiel 100 Euro in Richtung Sparplan ab und am Ende fließt Dir der Gesamtbetrag wieder zu. In Excel kannst Du mit der IKV-Funktion den „internen Zinsfluss“ oder „Zinsfuß“ solcher Geldströme berechnen. Meine Empfehlung ist: baue Dir damit ein Excelblatt. Das ist schnell gemacht.
Oder vielleicht doch lieber eine Wohnung kaufen? Oder Gold?
Solch ein Excelblatt kannst Du auch für andere Investitionen wie zum Beispiel für den Kauf einer Wohnung oder für die Bewertung eines Bausparvertrages, von der Spar- bis zur Darlehensphase, nutzen. Du erfasst in einer Spalte alle zunächst abfließenden und später eingehenden Zahlungsströme und berechnest dann den Zinsfluss mittels IKV-Funktion.
Diese Themen sind jedoch nicht meine Schwimmbahn. Anders als zum Beispiel in den USA sind in Deutschland die Daten zu Immobilienpreisen leider nicht transparent und öffentlich zugänglich. Für diesen Blog nutze ich öffentlich zugängliche Daten. Wenn Du also Ideen für Finanzmodellierungen einer Investition suchst, dann musst Du anderweitig fündig werden.
Und Gold?
Das wiederum ist sehr einfach: für die Variable „stock“ oben setzt Du „GC=F“ ein. Das ist das Symbol für den Goldpreis. Und schon hast Du Dein Gold-Renditedreieck.
Zur Berechnung des „Zinsfußes“
In R verwende ich das Paket jrvFinance und die irr()-Funktion („internal rate of return“). Ich möchte hier meine Vorgehensweise möglichst genau darstellen (ein großer Vorteil von R, Python & Co), sodass Du meinen Ansatz überprüfen kannst. Wenn ich einen Fehler mache, dann bitte ich um einen Hinweis!
Ich investiere jeden Monat den Wert 1 in ein Wertpapier, das zu diesem Zeitpunkt je Anteil beim Kurswert x steht. Das heißt: ich erwerbe 1/x Anteile. Wenn ich nun Monat für Monat den Wert 1 investiere, dann muss ich die Kehrwerte 1/x über alle Monate aufsummieren, um zu berechnen, wie viele Anteile ich im Laufe der Zeit erworben habe. Diese Anteile verkaufe ich am Ende der Zeit zu dem dann gültigen Kurswert. So erstelle ich folgende Funktion, die mir aus
- dem „Einkaufskalender“ („schedule“: mit Spalten „Period“ und „Stock“)
- dem Startdatum („date1“) der Käufe und
- dem Verkaufsdatum („date2“)
den jeweiligen Zinsfuß berechnet:
Zinsfuss <- function(date1, date2) {
# Vektor aller Einkaufspreise:
buy <- schedule %>%
filter(Period >= date1,
Period < date2) %>%
pull(Stock)
# Anzahl der erworbenen Anteile:
shares <- sum(1/buy)
# Verkaufserlös:
sell <- shares*schedule$Stock[schedule$Period == date2]
# Da wir jeweils 1 investiert haben,
# ist unsere Investitition rentabel
# solange sell > length(buy) ist.
# Cashflow-Vektor:
my_cf <- rep(-1, length(buy)) %>% append(sell)
# Zinsfuss berechnen:
Zf <- jrvFinance::irr(my_cf)
# Das ist jedoch nur der monatliche Zinsfuss.
# Den müssen wir jetzt noch auf das Jahr umrechnen:
Zf.pa <- (1 + Zf)^12 - 1
return(Zf.pa)
}
Diese Funktion greift auf die in der Variablen „schedule“ abgelegten monatlichen Aktienstände zurück, die wir wie folgt aus dem Yahoo-Finance-Download, also der Variable „Stock“, berechnen:
schedule <- Stock %>%
mutate(Period = floor_date(Date, "1 month")) %>%
group_by(Period) %>%
filter(Date == min(Date)) %>%
select(Period, Stock)
Mit dieser Funktion Zinsfuss() durchlaufe ich nun eine Schleife über die gesamte Tabelle t2 und erhalte folgendes Rendite-Dreieck:
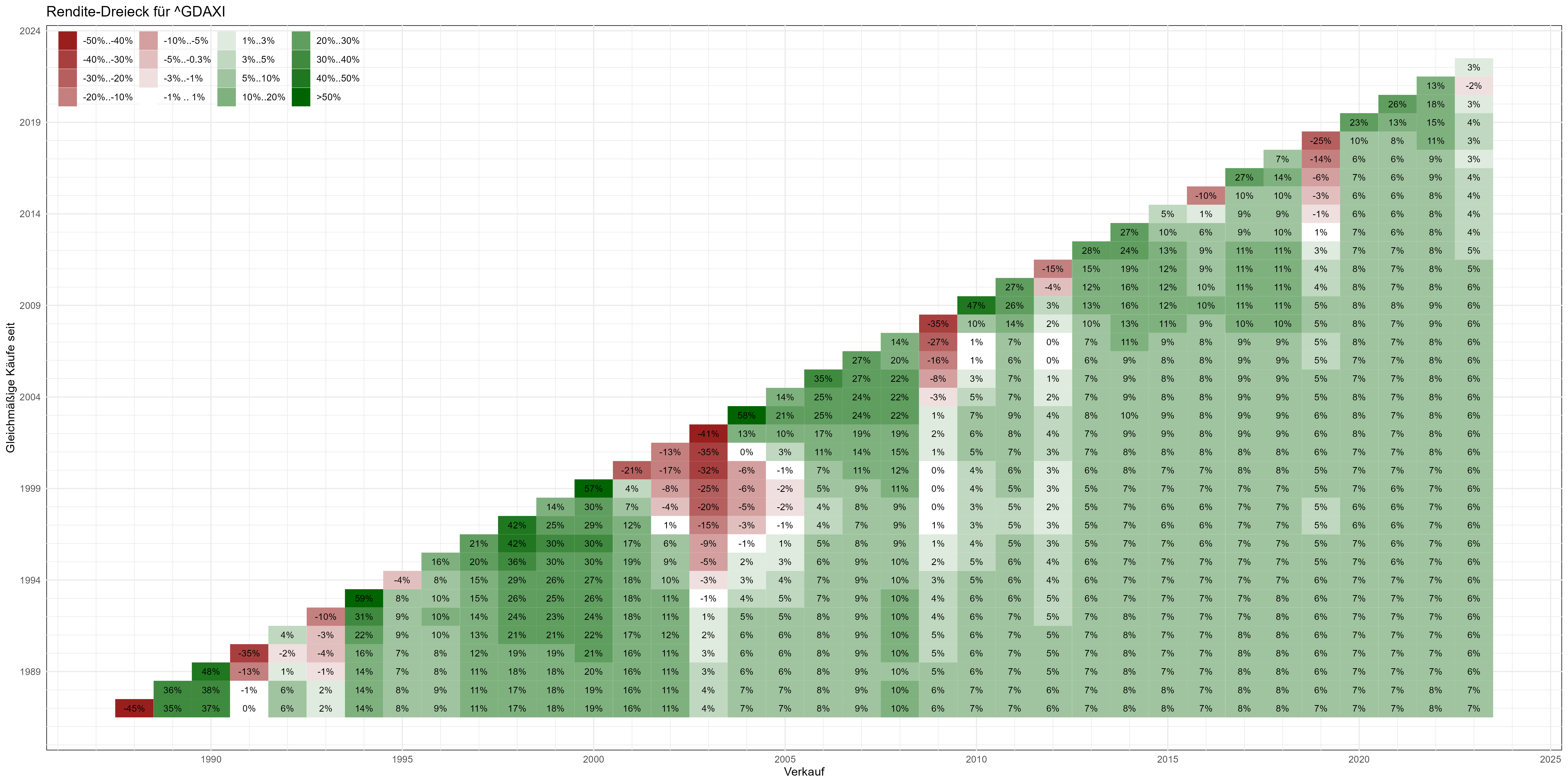
Rendite-Dreieck des Dax bei monatlich gleichbleibenden Zukäufen.
„Von weitem betrachtet“ sieht dieses Dreieck dem vorherigen recht ähnlich. Bei näherem Augenschein sind durchaus Unterschiede erkennbar: vor allem treten zu Krisenzeiten deutliche vertikale Strukturen hervor: da Du zu Krisenzeiten günstig nachkaufst, überstehst Du die Krisen schneller!
Durch regelmäßigen Nachkauf kannst Du Krisen „aussitzen“. Bei Nachkauf bei Bärenstimmung und dann günstigeren Preisen hat sich Deine Anlage schneller wieder „berappelt“ als bei einer Einmal-Investition.
Wärst Du zum Beispiel zum 1. 1. 2000 eingestiegen, dann hättest Du im ersten Jahr 21% Verlust gemacht. Bei Ausstieg am 1. 1. 2003 wärst Du sogar bei -32% p.a. gelandet. Gerade jetzt wäre aber „Ruhe bewahren“ richtig gewesen, denn bis zum 1. 1. 2006 hättest Du mit Deinen monatlichen Investitionen „im Schnitt“ einen Zinsfluss von 7% p. a. erwirtschaftet.
Dein „wahres“ Investitionsszenario ist noch entspannter
Der kontinuierliche Kauf „entschärft“ also das Problem der Volatilität. Gerade wenn Du Deine Anlage als Altersvorsorge betrachtest, dann wirst Du vermutlich auch nicht alles auf einen Schlag abziehen. Vielmehr wirst mit Rentenbeginn auch kontinuierlich, zum Beispiel monatlich, entnehmen: in Bullenjahren wenige, hochpreisige Anteile und in Bärenjahren mehr niedrigpreisige Anteile, um so einen monatlich gleichbleibenden Bedarf zu decken. Dadurch entspannt sich die Situation noch einmal. Das heißt:
Je länger und je kontinuierlicher Du investierst und gleichmäßiger Du entnimmst, desto mehr bildet Deine Investition die langfristige Entwicklung ab.
Wenn Du also glaubst, dass es mit der deutschen, der amerikanischen, der Weltwirtschaft langfristig bergauf geht, dann solltest Du über einen Rentensparplan in ein Papier, das Deinen bevorzugten Index nachbildet, ernsthaft nachdenken. Das Renditedreieck hilft Dir bei der Entscheidung.
Die Vergangenheit lässt keine Rückschlüsse auf die Zukunft zu
Zu recht magst Du nun sagen: Schön und gut – aber kann ich mich auch in Zukunft darauf verlassen, dass meine Anlage nach spätestens 10 Jahren wieder gut dasteht?
Die Antwort kennst Du selbst.
Nein, verlassen können wir uns auf die Zukunft nicht.
Es stehen große Herausforderungen an: Vielleicht wandert die deutsche Industrie ja dorthin ab, wo die Energie billiger ist. Oder wir kriegen die Digitalisierung nicht hin. Oder in Deutschland oder Europa entstehen „japanische Verhältnisse“. Oder die Klimakrise stürzt die ganze Welt in den Abgrund. Oder die USA versinken im Chaos. Oder, oder, oder.
Vielleicht. Und deshalb müssen wir die Ärmel hochkrempeln. Aussitzen können wir – als Menschheit – diese Themen nicht. „Als Menschheit“ haben wir aber auch andere Dinge hingekriegt: nach zwei Weltkriegen eine neue Wirtschaftsordnung aufgebaut, extreme Armut halbiert, Corona irgendwie überstanden. Vielleicht wird jetzt trotzdem alles anders und schlimmer. Oder aber wir kriegen das Problem mit dem Fachkräftemangel in den Griff. Vielleicht startet Deutschland auch dank künstlicher Intelligenz so richtig durch. Aber all das ist eine andere Geschichte. Und die musst Du mit jemand anderem besprechen, denn als „Schuster“ bleibe ich hier bei meinem „OSAN-Leisten“.
Wie Du Dich zu diesen Themen positionierst hat natürlich auch Konsequenzen für Deine Wahl. Denn falls Du in den DAX investierst, dann wettest Du darauf, dass es mit der deutschen Wirtschaft gut weiter geht. Vielleicht traust, nur als Beispiel, den USA mehr zu? Dann könntest Du den Dow Jones wählen. Oder Du siehst über die nächsten Jahrzehnte Indien oder China vorn? Dann suche Dir entsprechende ETFs aus und schaue ihre Rendite-Dreiecke an. Oder Du wettest einfach darauf, dass es mit der gesamten Welt „schon irgendwie weitergeht“? Dann könntest Du den MSCI World auswählen (der allerdings Nordamerika übergewichtet – schaue deshalb bei jedem ETF oder Fonds rein, was drin ist in der Packung).
Eine nützliche Faustformel
Was Du im Hinterkopf behalten solltest:
Eine Geldanlage, die zum Zinssatz x% verzinst wird,
verdoppelt nach etwa 70/x Jahren ihren Wert.
Bei 2% also nach 35 Jahren. Bei 5% schon nach 14 Jahren und bei 7% nach 10 Jahren. Wenn Du rechtzeitig anfängst und so Zeit mitbringst, dann solltest Du Dir diese Effekte nicht entgehen lassen. Vor allem, wenn Du erst in 40 Jahren in Rente gehst.
Ein paar Tipps möchte ich Dir noch mit auf den Weg geben
So schwer ist es also nicht, mit doppelt soviel Geld in Rente zu gehen. Und so „steinig und schwer“ ist der Weg dahin auch nicht, selbst wenn Du ihn alleine gehst: Du musst regelmäßig Geld beiseite legen, in guten wie in schlechten Zeiten „einfach weitermachen“ und am besten schließlich genauso kontinuierlich Geld entnehmen.
Ich denke jedoch auch, dass dieses Thema wichtig genug ist und dass Du eigene Recherchen anstellen, mit Freunden, Eltern und mit Deiner Bank darüber sprechen solltest.
Meine „Schwimmbahn“ ist die Visualisierung von Daten. Die folgenden Gedanken möchte ich Dir dennoch nicht vorenthalten, da sie Dir helfen können, Dich auf diese Gespräche vorzubereiten. Du solltest sie aber unter dem Vorbehalt lesen, dass ich hier meinen Kompetenzbereich verlasse.
Bevor Du bei der Bank unterschreibst: Frage nach, welche Möglichkeiten deren Anlage Dir für Spar- und Entnahmephase bietet (z. B. die Möglichkeit, auch einmal auszusetzen, ganz auszusteigen oder eine größere Einzahlung zu tätigen) und wie hoch die Kosten dafür sind. Bei 5% Ausgabeaufschlag und 2% Verwaltungsgebühren pro Jahr muss ein Fonds schon richtig gut gemanagt sein, um „den Markt“, also den von Dir für einen ETF gewählten Index, zu schlagen. Bei all den zusätzlichen Features wie „Airbag“, „dynamische Anpassungen ohne zusätzliche Gesundheitsprüfung“ und „eingebaute Berufsunfähigkeitsversicherung“ lässt sich vielleicht gar nicht so genau sagen, wie hoch diese Gebühren tatsächlich sind. Dann ist für Dich der Geldfluss wichtig, den Du in Excel mit der IKV-Funktion in den Griff kriegst. Und stelle die Frage: ich schließe heute ab und verkaufe morgen wieder. Wieviel kriege ich zurück? – Denn DAS ist der Ausgabeaufschlag.
Eine weitere Idee Deiner Bank könnte sein, das Geld „zur Sicherheit“ mehreren Managern anzuvertrauen („lege niemals alle Eier in einen Korb“). Bei diesem Vorschlag solltest Du folgendes überlegen: Alle Manager zusammen bilden den Markt ab: manche performen besser, manche schlechter. Wie viele verschiedene Manager musst Du im Portfolio haben, um den Markt tatsächlich mehr oder weniger abzubilden? „Zur Sicherheit“ zehn? – Vielleicht kannst Du Dir dann die Verwaltungsgebühren für diese Manager auch sparen und gleich einen Index-ETF kaufen.
Aber Achtung: ETF ist nicht gleich ETF, auch wenn die Gebühren vernachlässigbar sind. Das siehst Du auch, wenn Du deren Renditedreiecke rechnest (sehr einfach: Du änderst die Variable „stock“ in dem Code oben).
Hier sind noch meine eigenen „Leitplanken“ für Investitionen – zum Teil habe ich dafür Lehrgeld bezahlt, das Du Dir vielleicht sparen kannst:
- Ich kaufe ETFs nur zu transparenten und gut regulierten Märkten. Übersetzt für mich heißt das, dass ich mich auf demokratisch regierte Länder beschränke.
- Ich bin vorsichtig bei „Nischen-ETFs“. Vieles klingt gut („Wasserstoff“, „ökologisch“, „sozial“, …). Und es ist sicher richtig, auf solche Trends zu setzen, wenn man an sie glaubt. Wenn mein „Traum-ETF“ aber eine Nische besetzt (wenige, kleine Unternehmen) und viele andere meinen Traum teilen, dann kann durch eben diese Anlagemöglichkeit die Nische „hochgejazzt“ werden – und es entsteht ein Blase. Ich schaue mir also an, welche und wie viele Unternehmen drin sind in dem ETF, wo sie beheimatet sind und wie groß sie sind.
Die Idee, die wir hier verfolgen, ist ohnehin: lasst uns nicht zu clever sein. Wir sind lieber konsistent (regelmäßig anlegen, liegen lassen, viel später regelmäßig entnehmen). Denn wenn Du auf den „Geheimtipp-ETF“ setzt, dann sagst Du ja insgeheim doch, dass Du schlauer bist als der Markt. Oder?
Ein Nachtrag noch: am 8. Juni hat die FAZ einen meiner Ansicht nach guten Artikel genau zu diesen Fragen veröffentlicht: „Sind ETFs wirklich besser?“. Vielleicht steigst Du damit einmal ein.
Wo ich Unterstützung gebrauchen kann
Es gelingt mir nicht, die exakten Werte des Rendite-Dreiecks für den MSCI World in dem oben zitierten Artikel der FAZ nachzubauen. Vielleicht wird mit einem anderen Stichdatum als dem 1. Januars gerechnet? Meine Zahlen erscheinen zudem allgemein etwas niedriger als die des Deutschen Aktieninstituts zu sein. Ist meine Zinsfußberechnung vielleicht doch falsch? Die Schlussfolgerungen bleiben die gleichen. Aber diese Unstimmigkeit würde ich gerne aufklären.
