Die „Python Challenge“
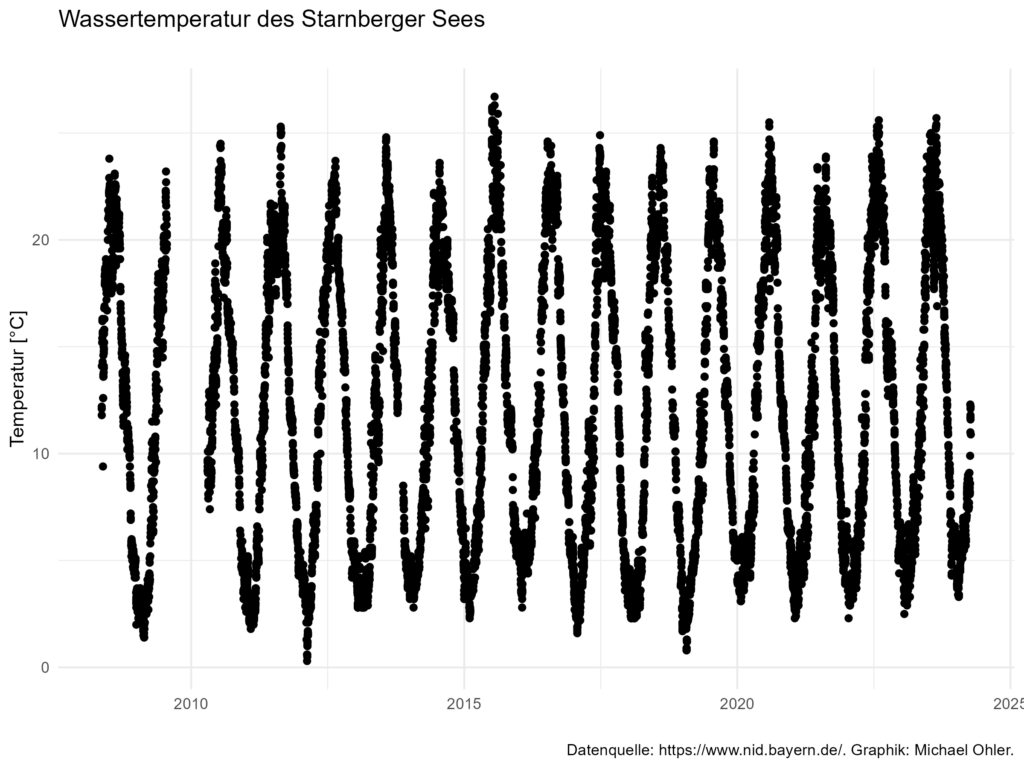
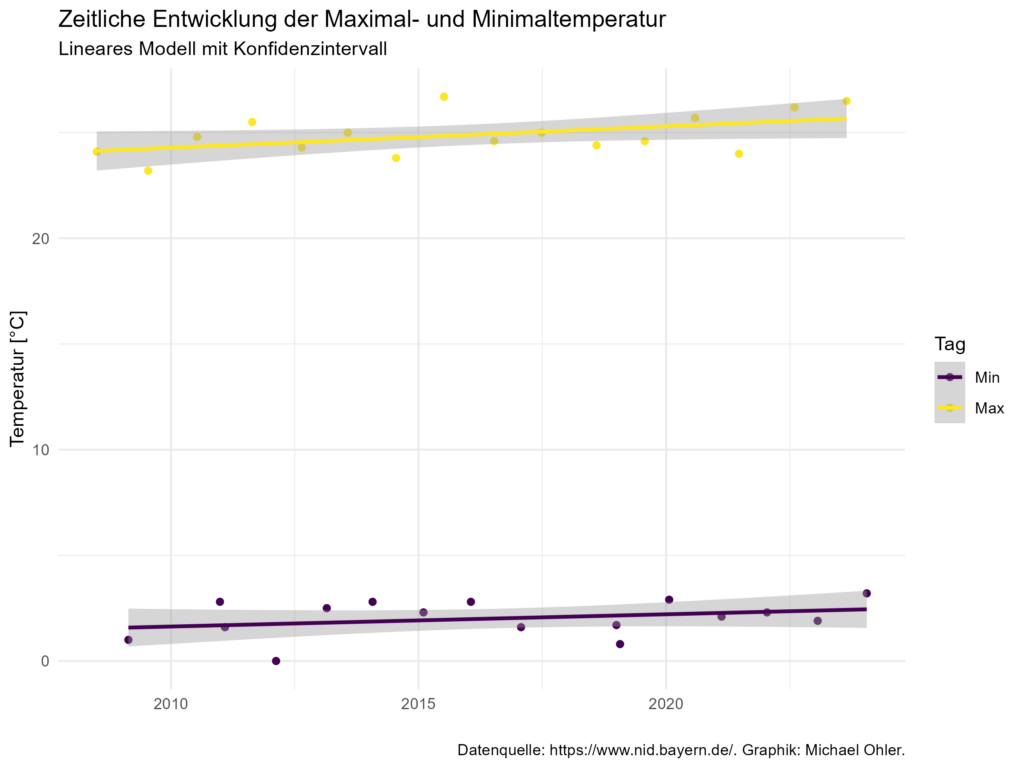
In meinem letzten Beitrag habe ich Temperaturdaten des Starnberger Sees untersucht und mit einer recht hemdsärmeligen Methode eine Erwärmung über den Betrachtungszeitraum gefunden. Allerdings habe ich für diese Untersuchung jeweils nur den Höchst- und den Tiefstwert eines jeden Jahres verwendet und so aus dem reichen Schatz der Daten mit mehr als 133000 Messwerten von über 5500 Tagen nur einen verschwindend kleinen Teil der Information, nämlich die jeweiligen Höchst- und Tiefstwerte eines jeden Jahres, genutzt. Wenn Du Dich mit Daten beschäftigst, dann würde auch Dich das wurmen.
Deshalb möchte ich heute nachlegen. Es geht mir zunächst um eine graphische Darstellung. Dafür habe ich ein wenig „knobeln“ müssen und einige Methoden ausprobiert. Und ich war froh, dass mir dazu die Analysesprache R zur Verfügung steht. Da ich mich derzeit auch in Python einarbeite und ich, zumindest was die graphischen Möglichkeiten angeht, noch nicht so ganz zufrieden bin (was auch an meinen begrenzten Fähigkeiten liegen mag), möchte ich gerne eine „Python Challenge“ aussprechen:
Kannst Du, kann irgend jemand mit vernünftigem Aufwand die folgenden Graphiken in Python nachbauen? Meinetwegen können wir auch Excel, Minitab, SPSS & Co mit einschließen. Ich glaube aber, diese Werkzeuge scheiden schon an der Startlinie aus. Schreib‘ mich gerne an, wenn es Dir gelingt!
Zunächst geht es hemdsärmelig weiter
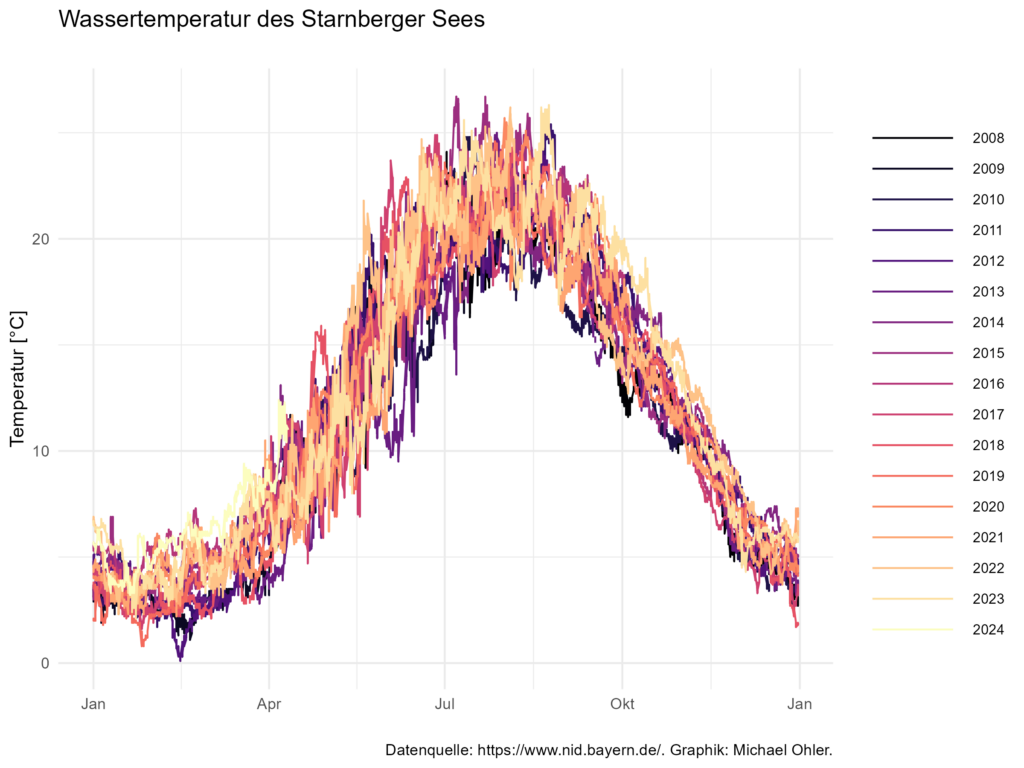
Die Schwierigkeit der Analyse besteht darin, dass die Temperatur des Sees jahreszeitlichen Schwankungen unterliegt: Im Winter ist das Wasser kalt und im Sommer warm. Es gibt zudem sowohl kalte als auch warme Sommer und Winter. Und auch die Erwärmung im Frühling oder die Abkühlung im Herbst könnte früher oder später einsetzen. Wie also macht man einen langfristigen Trend, so es ihn denn gibt, sichtbar?
Die „richtige“ Herangehensweise wäre, Werkzeuge der Zeitreihenanalyse wie ARIMA zu verwenden. Vor mehr als 15 Jahren habe ich mich darin eingearbeitet, das jedoch nie wieder verwendet. Deshalb möchte ich mich zunächst einmal darum „herummogeln“ und schauen, wie ich eigenhändig weiterkomme. Vermutlich im nächsten Beitrag werde ich mich dann um diese Werkzeuge kümmern.
Der Vergleich zu den Vorjahren
Eine erste Idee besteht darin, den jeweiligen Tag eines jeden Jahres zu nehmen. Der erste Januar ist der Tag 1 und der 31. Dezember der Tag 365. Wir könnten dann Tag für Tag die Mittelwerte der vergangenen 5 oder auch 10 Jahre berechnen und dieser Mittelwert mit dem im Folgejahr am Vergleichstag gemessenen Wert vergleichen.
Das habe ich ausprobiert. Da aber eben die Erwärmungs- und Abkühlungsphasen mal früher und mal später einsetzen, führt das zu einer höheren Variation dieser Mittelwerte und damit der Referenzwerte.
Deshalb habe ich das Zeitfenster des Vergleichs variabel gemacht. Sagen wir, ich möchte wissen, ob der See am Tag 109 dieses Jahres (am heutigen 18. April) im Vergleich zu den Vorgängerjahren eher wärmer oder eher kälter war. In meinem Code kann ich jetzt einstellen, dass ich einstellbar zum Beispiel 5 oder 10 Jahre zurückschauen möchte. Ich kann auch einstellen, dass ich für den Vergleichszeitraum aus jedem dieser Jahre ein Zeitfenster von plus und minus beispielsweise 14 Tagen auswählen möchte. Über all diese Tage berechne ich dann den mittleren Wert (Median) und die typische Variation (Standardabweichung). Da die Messbehörde an manchen Tagen besonders „fleißig“ war und häufiger als sonst die Wassertemperatur gemessen hat, habe ich vorher den Mittelwert all dieser Tageswerte gebildet, um nicht bestimmte Tage bevorzugt zu berücksichtigen, nur weil an ihnen häufiger gemessen wurde.
Um zu beurteilen, ob der heutige Wert stark von der Vergangenheit abweicht, vergleiche ich den Unterschied zwischen historischem Median und heutigem Messwert mit der Standardabweichung dieser historischen Vergleichswerte: Liegt der Unterschied zwischen plus/minus einer Standardabweichung, dann sage ich: alles gut, das kommt vor. Eine Abweichung um eine, zwei, drei oder mehr Standardabweichungen nach oben oder nach unten zeigt hingegen eine immer stärkere Auffälligkeit an. In der folgenden Graphik stelle ich das bildlich dar. Die Farbbänder geben dabei die Bänder von einer, zwei und drei Standardabweichungen in beide Richtungen an: warme Farben für Abweichungen nach oben und kalte für Abweichungen nach unten.
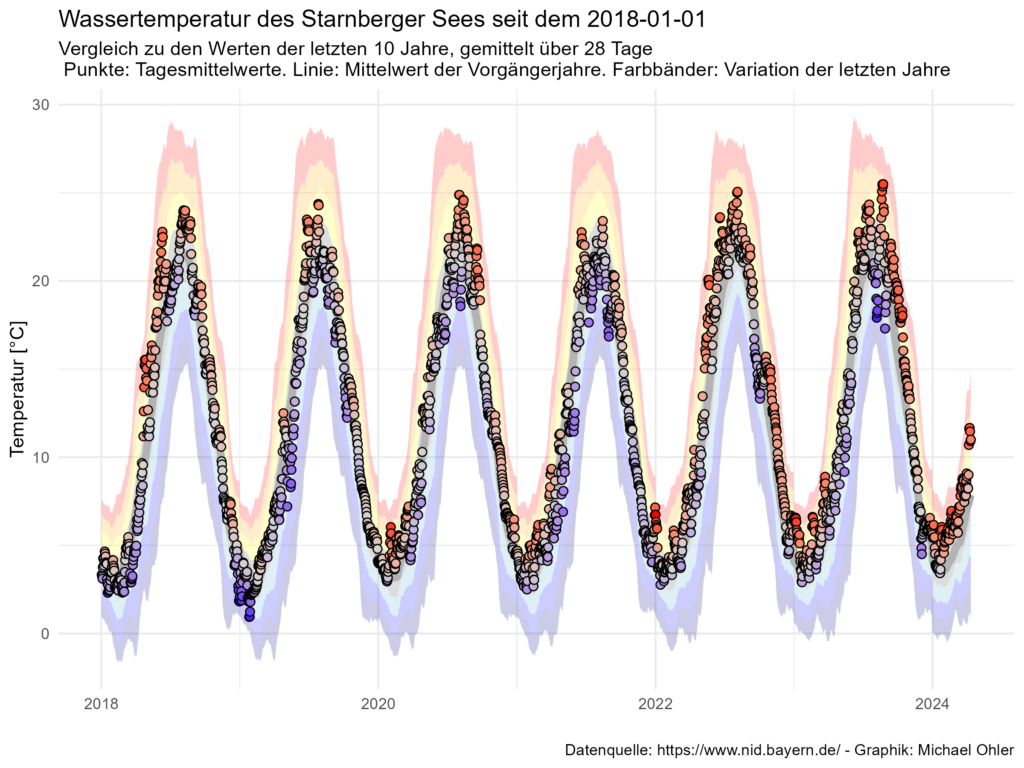
Zugegeben: das ist eine nicht ganz leicht verdauliche Graphik. Du kannst sie wie folgt lesen. Wenn eine Abkühlungsphase wie im Herbst 2022 vor allem rötlich gefärbt ist, dann hat sich der See in dem Jahr später als früher abgekühlt. Für die Sommermonate dominiert über alle Jahre hinweg die rote Farbe: die Sommer sind wärmer geworden. Auch die Tiefpunkte im Winter sind – mit Ausnahme des Winters 2019 – vor allem durch wärmere Temperaturen geprägt.
Interessant sind auch Phasen, an denen die Temperaturpunkte zwischen rötlichen („wärmer als in den 10 vorherigen Jahren“) und bläulichen („kälter als vorher“) Farbtönen springen. Das siehst Du zum Beispiel für den Winter 2022/2023. Ich halte das nicht für Fehler oder Ungenauigkeiten in den Daten. Wer einmal im Starnberger See weiter hinausgeschwommen ist, der weiß, dass es recht kräftige Strömungen gibt. Ich nehme also an, dass wir hier den Effekt von sich – aufgrund von Wind und Wetter – ändernden kalten und warmen Strömungen sehen. Diese Effekte werden bei der Mittelwertbildung „herausgemittelt“, sind aber bei den Tagesdaten durchaus vorhanden.
Die folgende Graphik zeigt aus der vorherigen Graphik den Ausschnitt seit Beginn dieses Jahres:
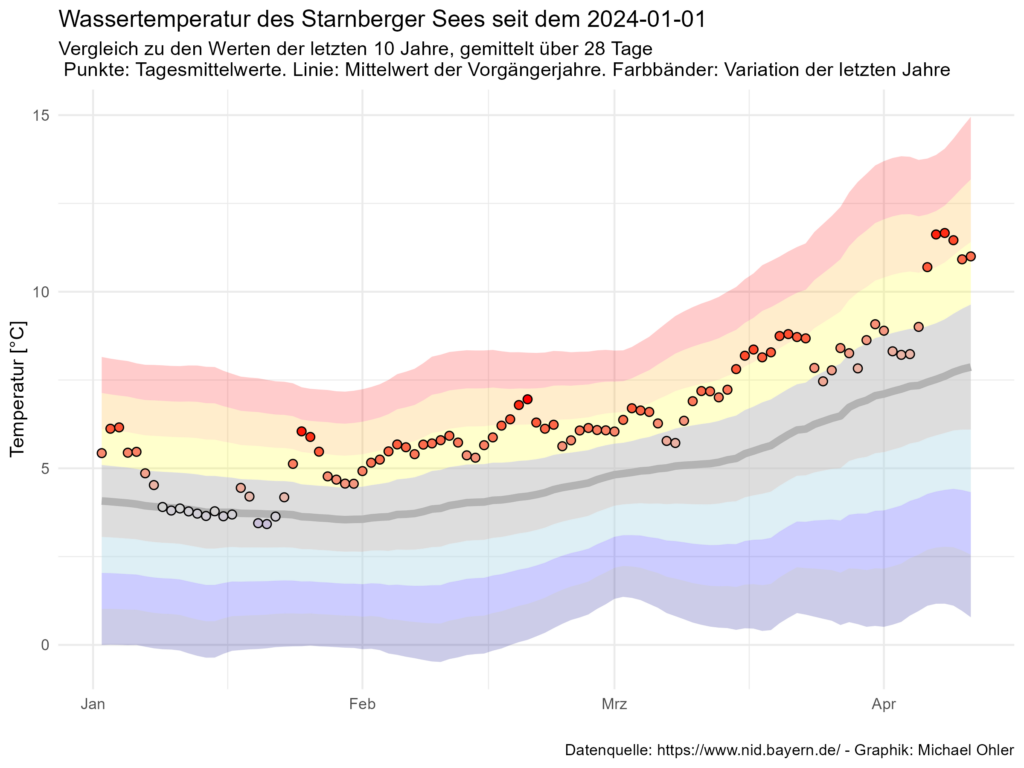
Sehr deutlich erkennbar liegen die Temperaturen deutlich über denen der Vorgängerjahre – und es ist kein Wunder, dass mein Freund Christian am letzten Wochenende bei behaglichen 12°C Wassertemperatur die Badesaison eröffnet hat. Diese Temperaturen liegen in dem orange dargestellten Band von zwei bis drei Standardabweichungen über dem mittleren Wert der Vorgängerjahre.
Um wie viel ist der See nun „wirklich“ wärmer geworden?
Das ist tatsächlich eine kniffelige Frage und ich habe einige Zeit gebraucht, um eine mir sinnvoll erscheinende Methode der Bewertung zu finden. Wenn Du die obere erste Graphik betrachtest, dann siehst Du, dass die Temperaturwerte mal nach oben (rot) und mal nach unten (blau) abweichen. Du kannst nun sagen: „Ja klar, das kommt natürlich vor. ‚Im Schnitt‘ gleicht sich das aber aus“.
Wenn dem so wäre, dass sich das „im Schnitt ausgleicht“, dann sollten sich die Abweichungen nach oben und nach unten die Waage halten. Für die folgende Diskussion möchte ich Dir einen konkreten Blick auf die Daten geben:
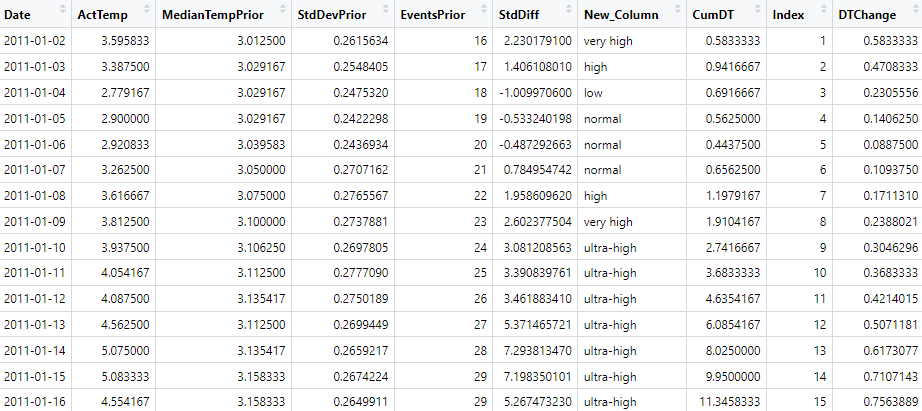
Du siehst hier das Datum, die „aktuelle Temperatur“ (gemittelt über alle verfügbaren Messwerte) an dem jeweiligen Tag, den historischen Median, die historische Standardabweichung und wie viele Tagesmittelwerte der Berechnung von Median und Standardabweichung zugrunde gelegen haben. In der Spalte CumDT („kumuliertes Delta der Temperatur“) rechne ich zunächst den Unterschied der Werte in Spalte 2 und 3 aus: das ist die jeweilige Temperaturabweichung. Für den 2. Februar beträgt sie 0.8333 Grad. Diese Abweichung addiere ich zu dem Temperaturunterschied des 3. Februar hinzu und erhalte dann 0.9417 Grad – und so weiter. Wenn sich diese Abweichungen nach oben und nach unten die Waage halten würden, dann würde diese Summe über die gesamte Tabelle hinweg berechnet klein bleiben. In der Spalte DTChange dividiere ich diese Summe noch durch den laufenden Index, also die Anzahl der Werte, die ich in CumDT bis zur entsprechenden Zeile aufsummiert habe. Am Ende des Betrachtungszeitraum steht so die „Nettoabweichung“ von aktueller zur historischen Vergleichstemperatur.
Dieses „Nettoabweichung“ lässt sich über den Betrachtungszeitraum hinweg auch graphisch darstellen:
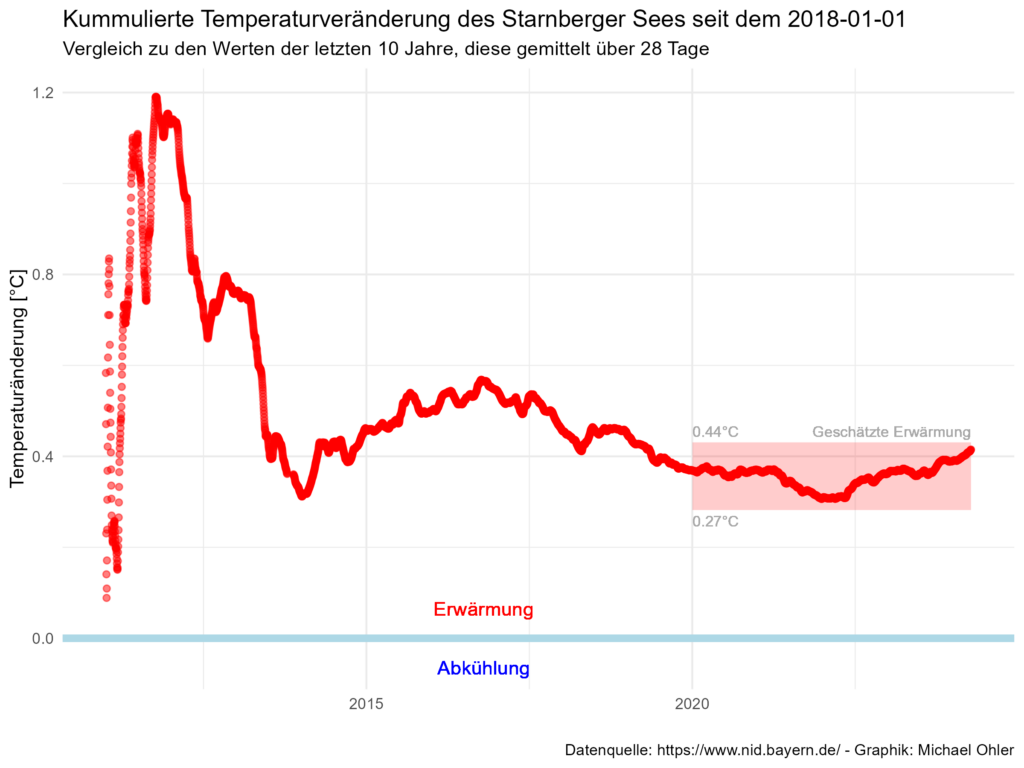
Zu Beginn steigen die Werte zunächst an: eine „Wärmephase“, dann fallen sie wieder ab, eine „Kältephase“. Je mehr Werte hinzukommen, desto weniger spielen solche Wärme- und Kältephasen jedoch eine Rolle, weil sie sich tatsächlich über den Betrachtungszeitraum hinweg „wegmitteln“. Allerdings schwingt sich die Kurve nicht um die Null-Linie (hellblau) herum ein. Sie liegt vielmehr durchgehend oberhalb und damit im Bereich der Erwärmung.
Ich verwende dann den Zeitraum seit dem Beginn des Jahres 2020, um diese Erwärmung abzuschätzen und berechne für diesen Zeitraum Mittelwert und Standardabweichung von DTChange. In der Graphik angezeigt ist der Bereich von plus/minus drei Standardabweichungen. So kommen wir zu der Aussage:
In den letzten 10 Jahren hat sich der Starnberger See tatsächlich erwärmt. Mit unserer hemdsärmeligen Methode ermitteln wir eine Erwärmung von ca. 0.3-0.4°C über einen Zeitraum von 10 Jahren.
Das mag nicht nach viel erscheinen und andere mögen beurteilen, welche Auswirkungen es hat. Aber es ist signifikant.
Lasst uns Umweltdaten aufbereiten!
Ich muss die Daten noch mittels ARIMA anschauen. Eine andere Idee besteht darin, auch neuronale Netze einzusetzen. Mal sehen, was ich im Laufe der nächsten Wochen bewerkstelligen kann.
Ich glaube jedoch, dass es auch jetzt schon losgehen kann: vielleicht finden sich beim Ammersee oder irgend einem anderen Gewässer Auffälligkeiten der Temperatur oder des Wasserstandes? Es liegen zu sehr vielen bayrischen und deutschen Gewässern Daten öffentlich vor. Sie müssen „nur noch“ analysiert werden.
Wenn Du bei einer Versicherung arbeitest oder in Gewässernähe bauen möchtest, dann könnten solche Analysen durchaus interessant sein. Aber vielleicht interessierst Du Dich auch „einfach nur so“ für den Fluss in Deiner Nähe und möchtest wissen, wie ungewöhnlich Temperatur oder Wasserstand heute im Vergleich zur Vergangenheit sind?
Melde Dich gerne, wenn Du Dich dafür interessierst!