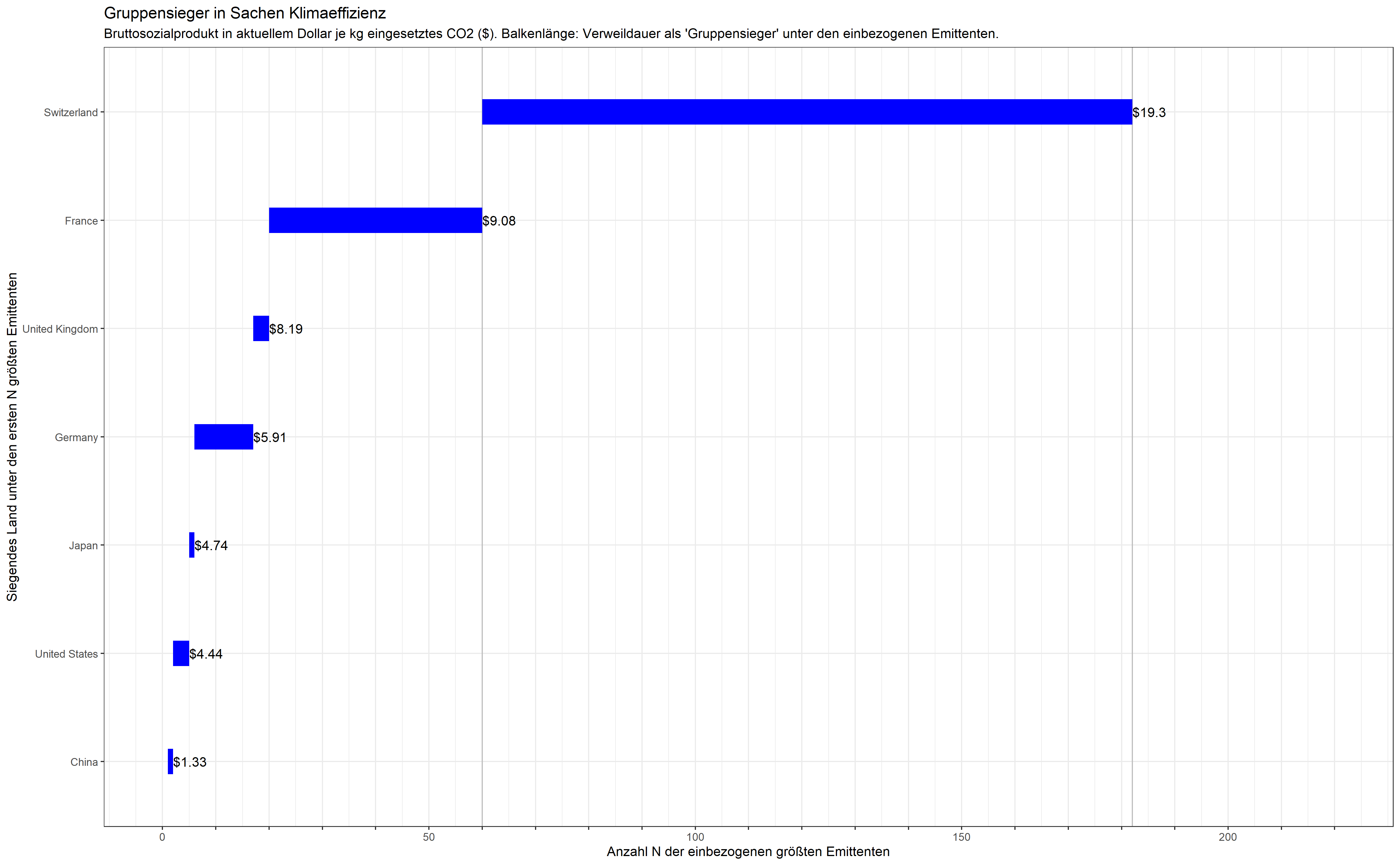
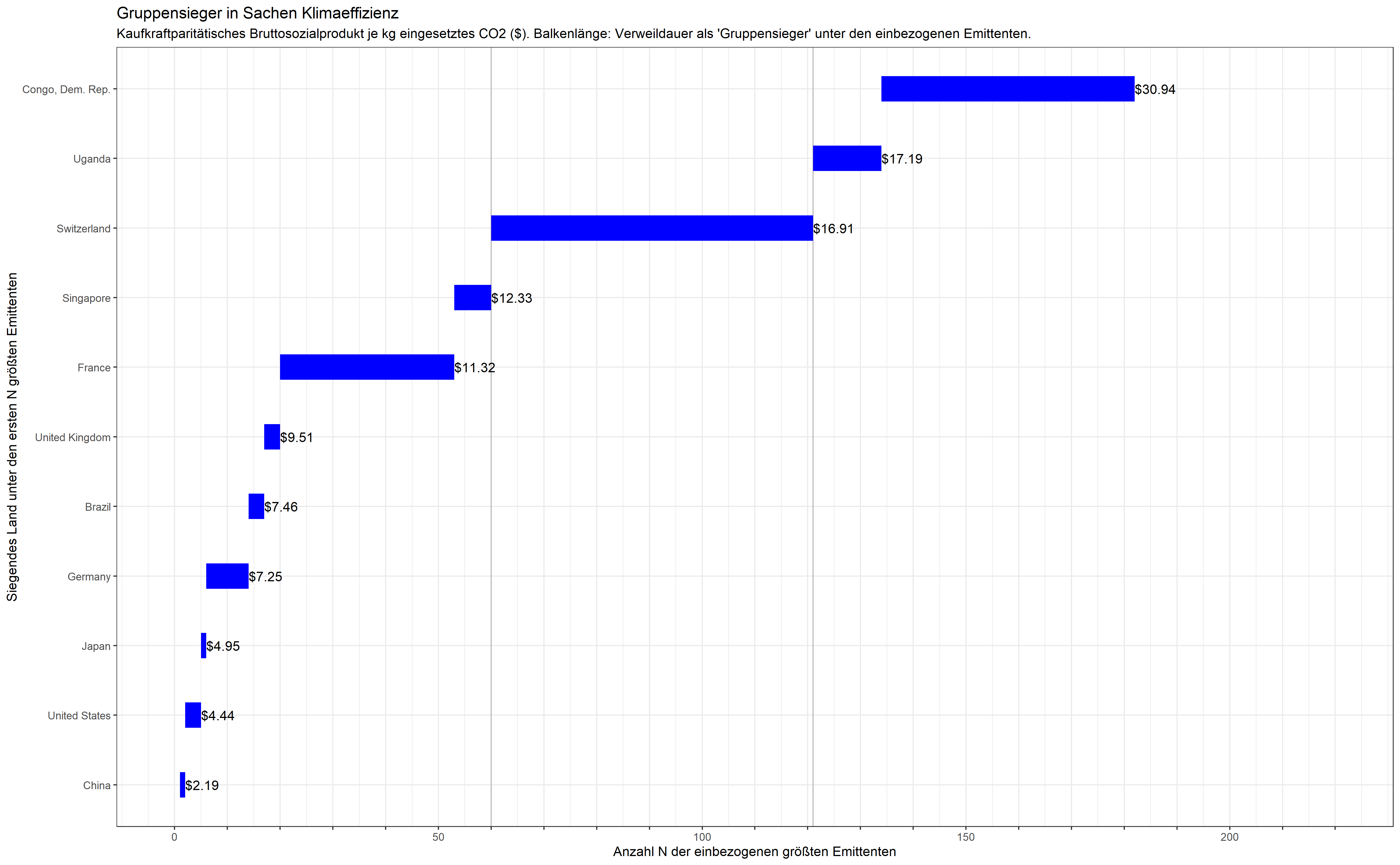
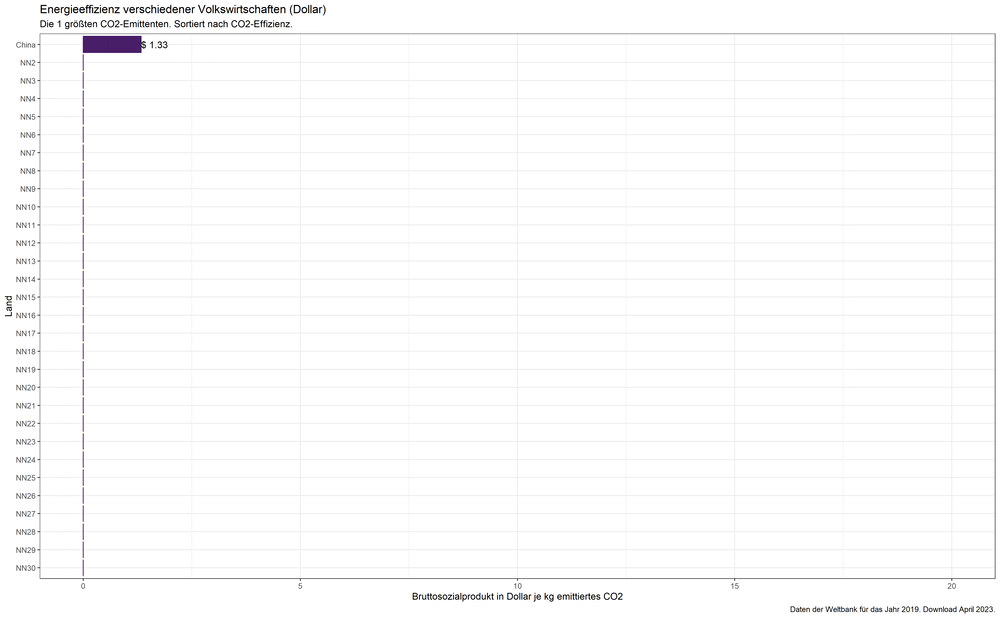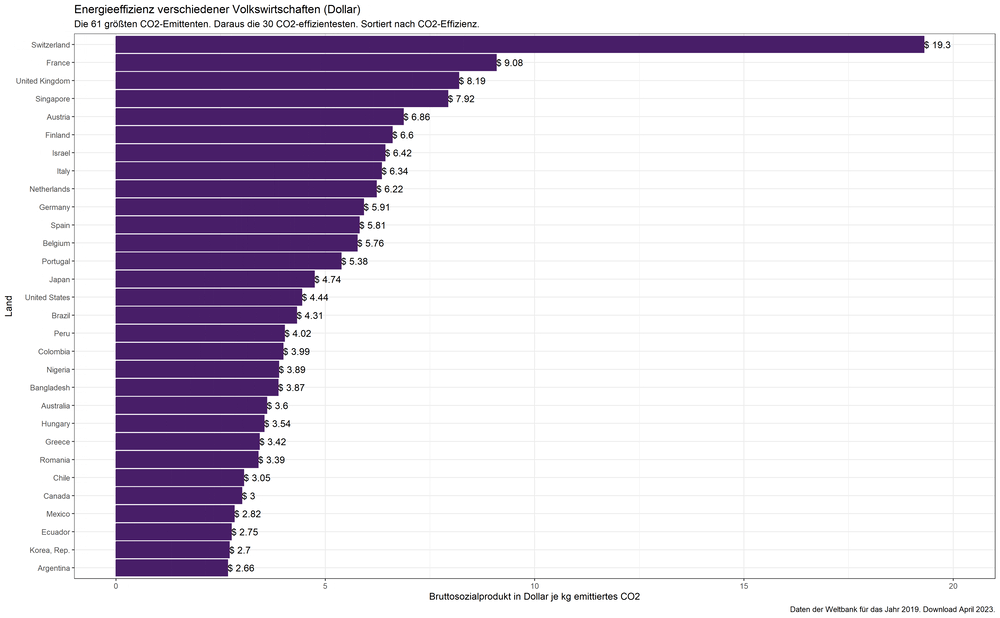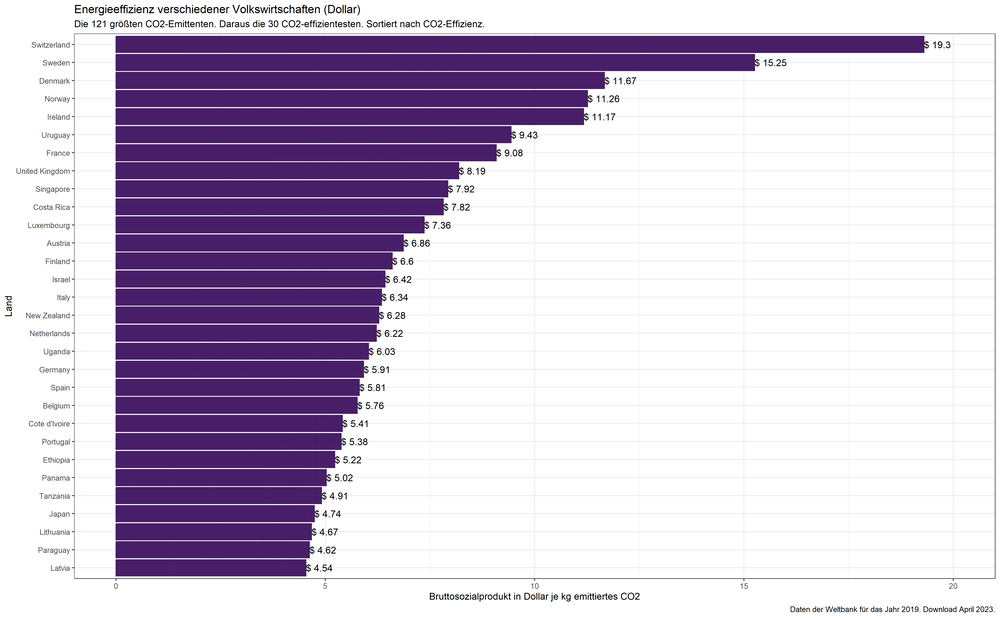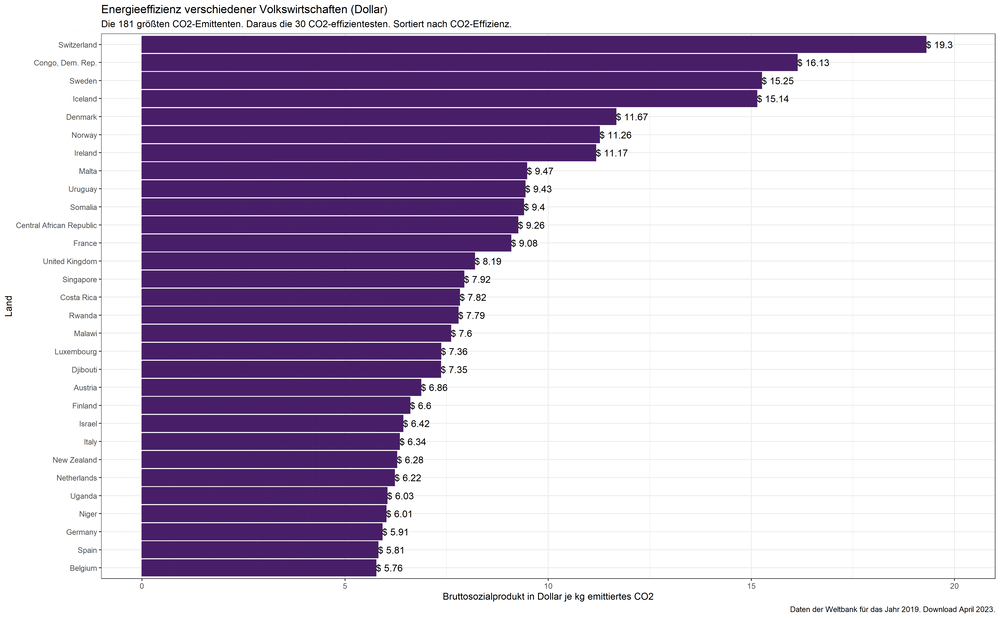
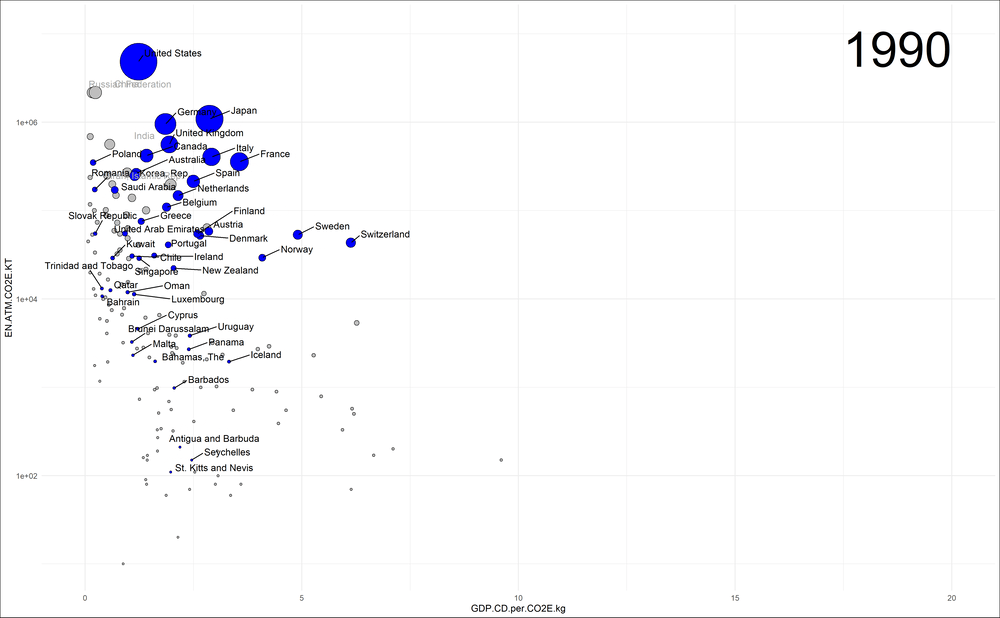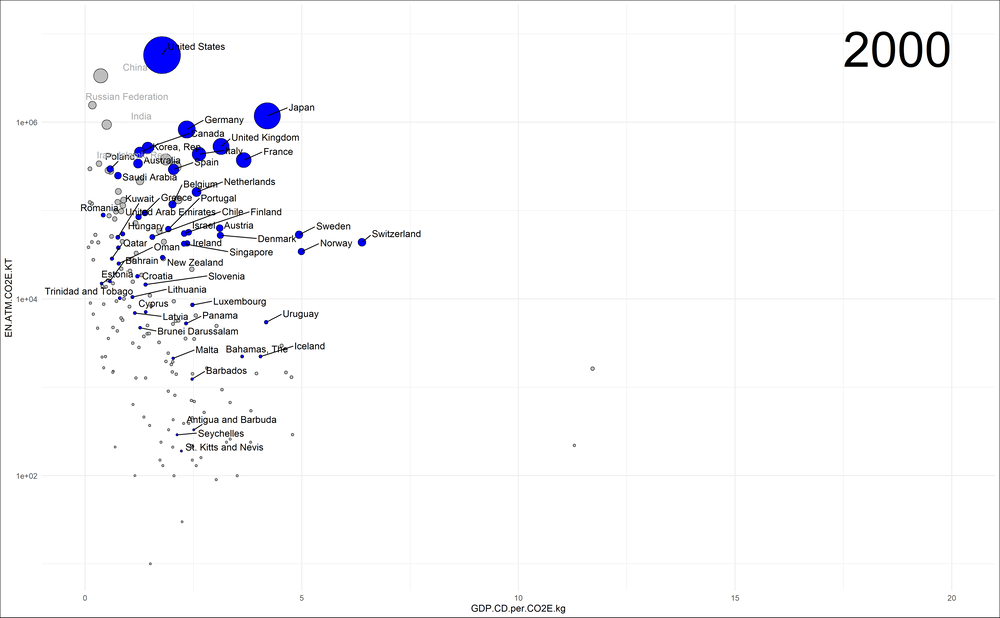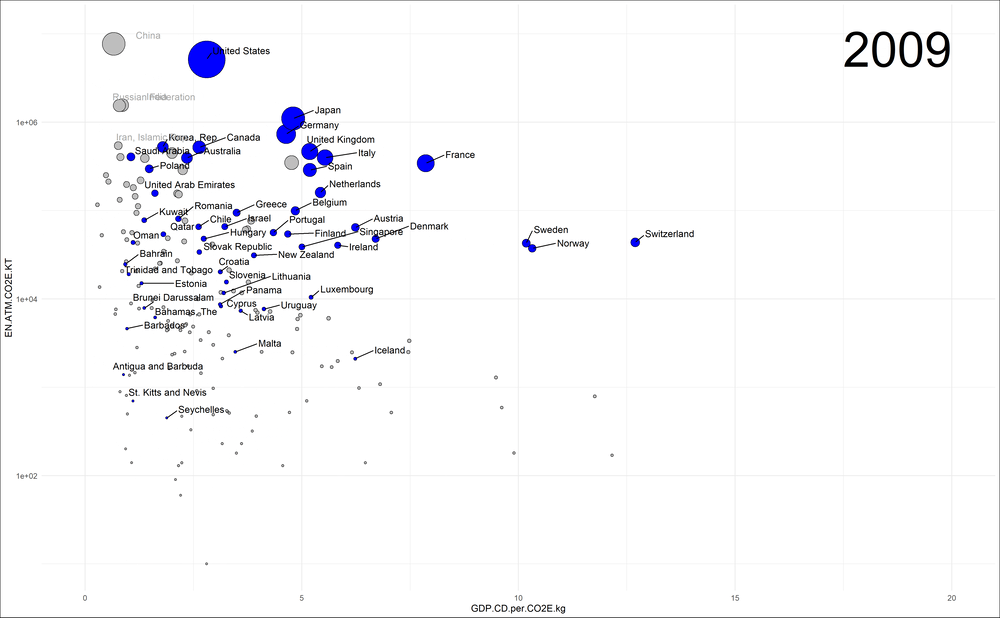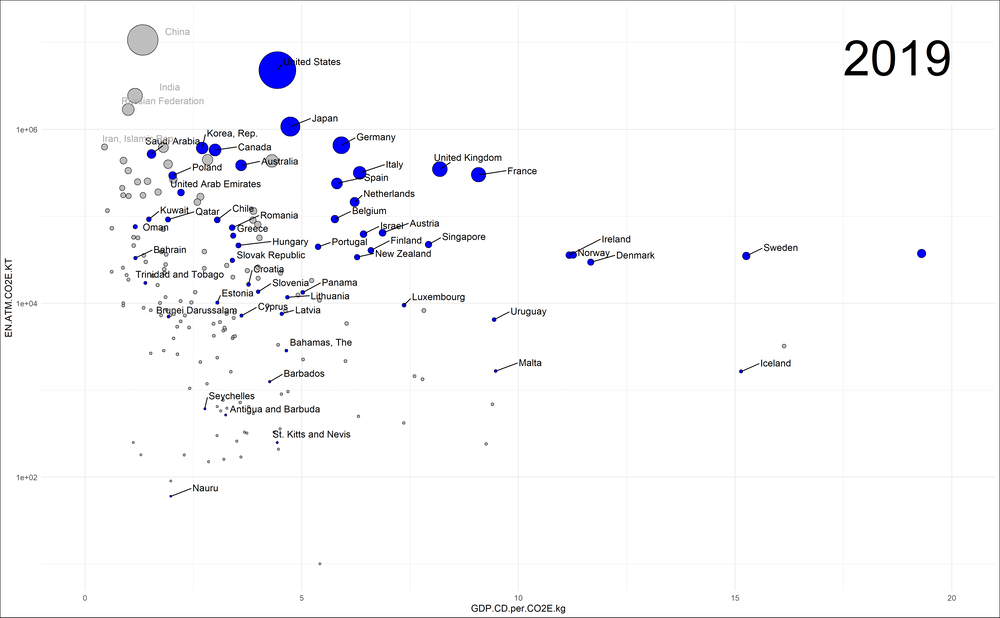
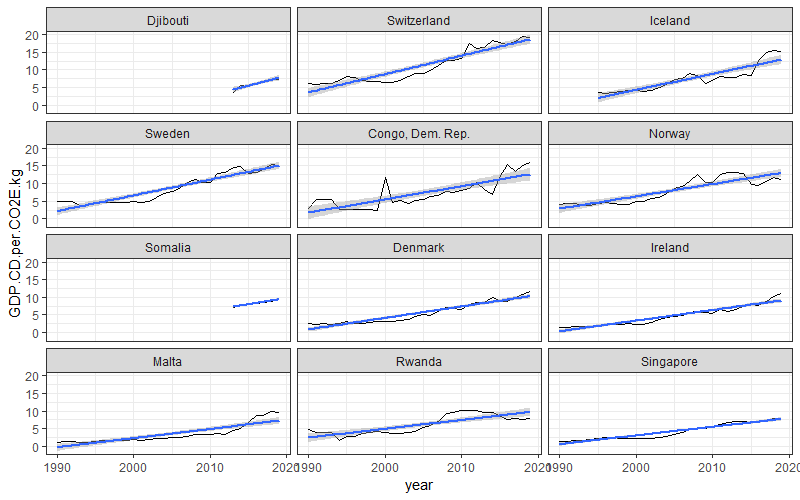
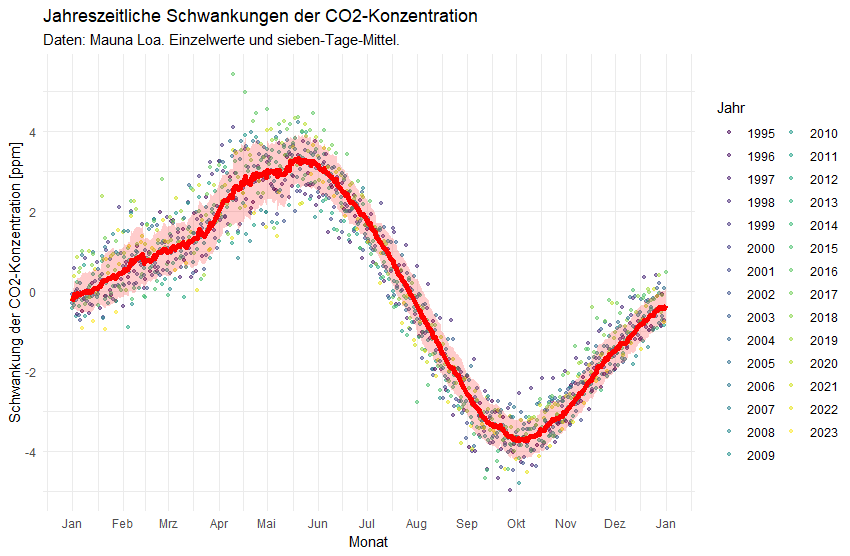
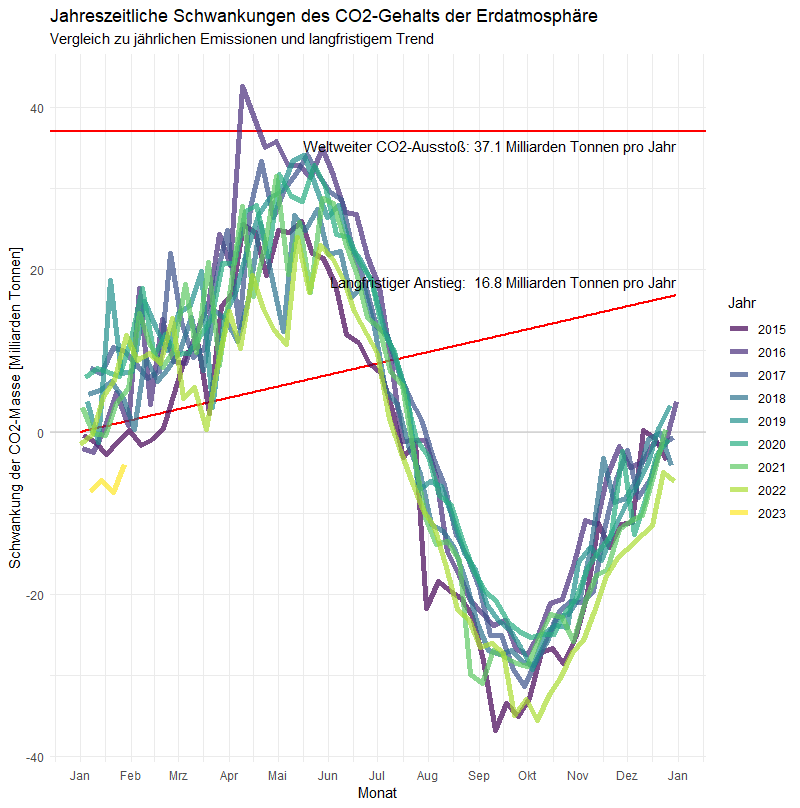
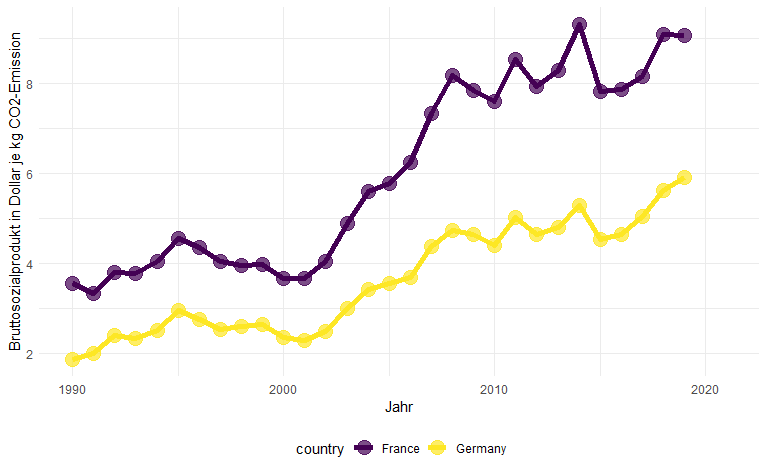
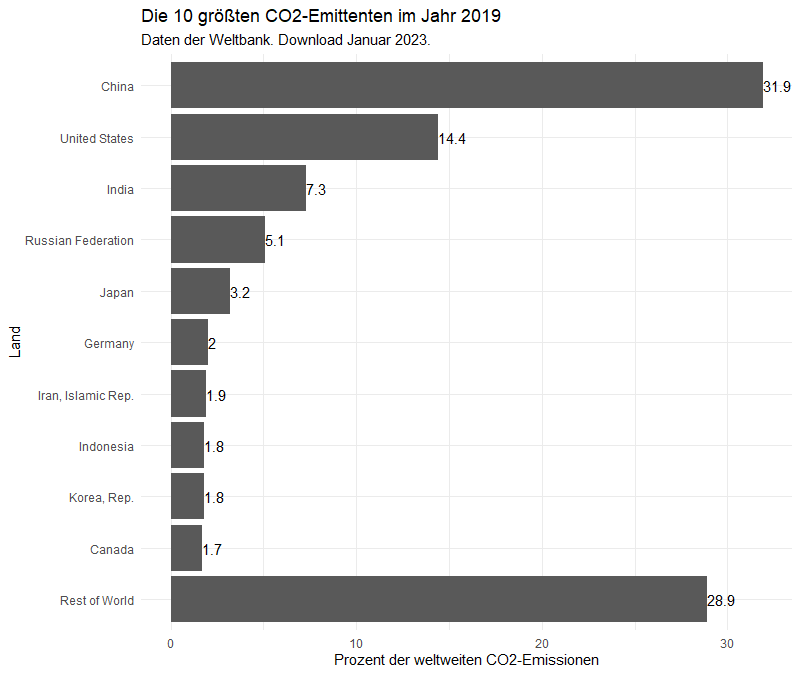
Was ist „Demokratie“?
Wie unterscheidet sie sich von anderen Regierungsformen?
Wie geht es weiter mit ihr?
Diese Fragen werden in der öffentlichen Debatte immer wieder aufgeworfen. Dabei bleibt so manches unklar, denn interessanterweise kommt der Begriff „Demokratie“ nicht einmal im deutschen Grundgesetz vor. Dort ist vielmehr von der „freiheitlich-demokratischen Grundordnung“ die Rede.
Warum Du diesen Beitrag lesen solltest
Wie auch immer Du Dich zum Thema „Demokratie“ positionierst: Du solltest darüber Bescheid wissen. Keine Lust auf dicke Bücher? Auch gut: wie wäre es dann mit Datenkolonnen? Die stehen nämlich öffentlich und in bestechender Qualität zur Verfügung. Und Du kannst sie für Deine Argumente nutzen. Das ist leichter – und inspirierender – als zu zunächst denken magst.
Demokratie – ein Auslaufmodell?
Manche halten die Demokratie für ein Auslaufmodell. Andere betrachten sie als „bedrohte Lebensform“ – so zumindest der Titel eines 2019 erschienenen Buches. Und Arte sieht sie „weltweit unter Druck“ – sehenswert: „Mit offenen Karten“ vom Mai 2022.
Wir wollen uns dem Thema auf Grundlage von Daten nähern. Das erscheint vor allem deshalb lohnend, weil dank der Initiativen von „State of Democracy“ und „Varieties of Democracy“ über Jahrzehnte hinweg umfangreiche Daten zu nahezu allen Ländern vorliegen.
Heute möchte ich
- anhand dieser Daten Fragestellungen zu Regierungsformen diskutieren
- darstellen, wie wichtig auch die Demokratisierung der Datenanalyse ist
- Dir helfen, diesen emotional geführten Debatten faktische Grundlagen zu geben.
Es ist heute auch etwas mehr geworden und Du solltest etwa 15-20 Minuten Zeit für die Lektüre mitbringen. Oder Du hangelst Dich anhand der Überschriften und Bildunterschriften durch. Am Ende fasse ich alles noch einmal zusammen.
Los geht’s!
Hintergrund zu den Daten und zu meinem Anliegen
Wenn Du möchtest, dann kannst Du die Daten von „State of Democracy“ in Excel- oder csv-Format herunterladen. Sie sind hier genau beschrieben. Mein vorheriger Beitrag gibt Dir eine kurze Übersicht.
Wenn Du bisher Daten mit Excel & Co analysiert hast, dann solltest Du das jetzt unbedingt auch versuchen – denn das ist im vorliegenden Fall eine wahre Plackerei und Du wirst nicht weit kommen. Moderne Fertigungs- und Transaktionsdaten sind in der Regel übrigens zumindest ähnlich komplex. Meine Hoffnung ist, dass Dich das motiviert, das Coden mit R oder Python zu erlernen. Wenn Du unabhängig sein und eigene Fragestellungen beantworten möchtest, dann kommst meiner Ansicht nach ohnehin nicht mehr darum herum.
Ich werde deshalb die wesentlichen Skriptzeilen einfügen und erläutern: Coden ist kein Hexenwerk – nicht zuletzt, weil Dir dabei zunehmend freundliche KI-Helferlein wie z.B. ChatGPT zur Seite stehen.
Wie wir die Daten auswerten
Ich verwende die Skriptsprache R, die speziell für die Handhabung von Daten, Texten und zunehmend auch Bildern entwickelt wurde. Du kannst Sie kostenfrei installieren und hast so auf einen Schlag Zugang zu den neuesten und besten Analysewerkzeugen, wie sie zum Teil auch schon in moderner Bezahlsoftware zur Verfügung stehen. So bist Du flexibel, stets eine Nasenlänge voraus, kannst Dich mit einer großen Community austauschen – und Du bezahlst nichts. Der Preis besteht freilich darin, dass Du Skripte schreibst und nicht einfach „klicken“ kannst.
Schauen wir uns an, was das konkret bedeutet.
Wir beschaffen uns die Daten
Es mag sein, dass der folgende Link sich im Laufe der Zeit ändert und Du ihn aktualisieren musst:
link <- "https://www.idea.int/gsod-indices/sites/default/
files/inline-files/gsodi_v6.1_1975_2021.csv"
t <- vroom(link,
delim = ";",
locale = locale(decimal_mark = ","))
Das war’s. Wir haben die Daten.
Die Struktur der Daten
Die so erzeugte Tabelle t hat über 9000 Zeilen und mehr als 200 Spalten, eine Zeile je Land und Jahr. In den Spalten werden Daten zu dem Grad von Null bis Eins erfasst, in dem über 140 Attribute, Unterattribute und Indizes erfüllt sind. Auf höchster Ebene geht es um die Erwartungen, die Menschen an ihre Regierung haben:
- Repräsentative Regierung (CA_1, „representative government“)
- Fundamentale Rechte (CA_2, „fundamental rights“)
- Überprüfung der Regierung (CA_3, „checks on the government“)
- Unvoreingenommene Verwaltung (CA_4, „impartial administration“)
- Bürgerliche Beteiligung (CA_5, „participatory engagement“).
Menschen wollen gut repräsentiert werden. Sie wollen, dass ihre fundamentalen Rechte geschützt werden, dass die Regierungsarbeit überprüft wird, dass sie es mit einer unvoreingenommen Verwaltung zu tun haben und sich selbst beteiligen können. Das klingt vernünftig.
Nun wirst Du fragen:
„Fundamentale Rechte:
Das ist recht schwammig.
Was heißt das?“
Dazu kannst Du die „Unterattribute“ betrachten, die in diesem Fall sogar aus Unter-Unterattributen bestehen, für die wiederum „Indizes“ gemessen werden: eine zunächst verwirrende aber äußerst reichhaltige Vielfalt.
Erkunde die Daten selbst – mit dem „Democralyser“
Ich habe eine R-Applikation geschrieben, den Democralyser, mit dem Du diese Zusammenhänge selbst erkunden kannst. Dieses (externe) Video gibt Dir dazu eine kurze, englischsprachige Einführung. Bevor Du weiterliest oder weiterarbeitest, empfehle ich Dir, ein wenig mit dem Democralyser zu spielen. Eine Warnung meines Freundes Mehmet: das kann ganz schön süchtig machen …
Wir bereiten die Daten auf
„Aus methodischen Gründen“ wird das Attribut der bürgerlichen Beteiligung (C_A5) nicht auf höchster Ebene aggregiert. Ich nehme mir dennoch die Freiheit, den Mittelwert (rowMeans) der entsprechenden Unterattribute zu bilden. Für alle Indizes und Attribute entferne ich zudem die Spalten für die oberen und unteren Konfidenzintervalle, sortieren die verbleibenden Spalten, formatiere die Regierungsformen als Faktoren und nehme Ländergruppen („groups“, s.u.) wie EU, ASEAN, Afrika usw. heraus, die dankenswerterweise in den letzten Zeilen stehen:
t$C_A5 <- t %>%
select(starts_with("C_SD5")) %>%
rowMeans(na.rm = TRUE)
t <- t %>%
select(-starts_with(c("U", "L"))) %>% # upper/lower CL
select(starts_with(c("ID", "C_A", "C_SD", "v_")),
everything())
t$regime_status_name <-
factor(t$regime_status_name,
levels = c("Authoritarian regime",
"Hybrid regime",
"Democracy"))
t$democratic_performance_name <-
factor(t$democratic_performance_name,
levels = c("Authoritarian regime",
"Hybrid regime",
"Weak democracy",
"Mid-range performing democracy",
"High performing democracy"))
# TODO: nicht elegant, da hart auf Zeilenbasis codiert:
groups <- unique(t$ID_country_name)[175:203]
t <- t %>% filter(ID_country_name %notin% groups)
Grundsätzliche Eigenschaften der Daten
Die Anzahl demokratischer Länder ist seit über 20 Jahren stabil
Wir wollen uns zunächst anschauen, wie sich die Regierungsformen im Laufe der Zeit entwickeln:
t %>%
ggplot(aes(x = ID_year,
fill = regime_status_name)) +
geom_bar(position = "stack")
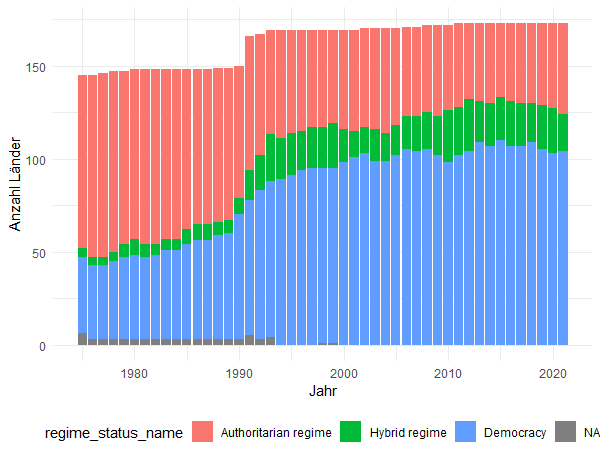
Regierungsformen im Wandel der Jahre
Unter dem Eindruck der oben zitierten Einschätzungen der Demokratie als „bedrohter Lebensform“, die „weltweit unter Druck“ ist, sind wir überrascht zu sehen, dass sie sich nicht auf dem Rückzug befindet, vielmehr:
In dem Zeitraum von Mitte der 1980er Jahre bis etwa zum Jahr 2000 ist die Anzahl der demokratisch regierten Länder stark angestiegen. Seither ist sie mehr oder weniger stabil.
Die Daten sind für alle Indizes normiert – mit einer Ausnahme
Schauen wir uns nun die Verteilung der Indizes an. Dafür stapele die Daten mit einer eigenen Funktion „my_stack(), um alle Werte in eine Spalte zu bringen und sie so allesamt in einem Histogramm darstellen zu können:
# TODO: ersetze diese Funktion durch eine dplyr-Lösung
t_stacked <- my_stack(t, c(9:154), c(1,3))
ggplot(data = t_stacked,
aes(x = values)) +
geom_histogram()
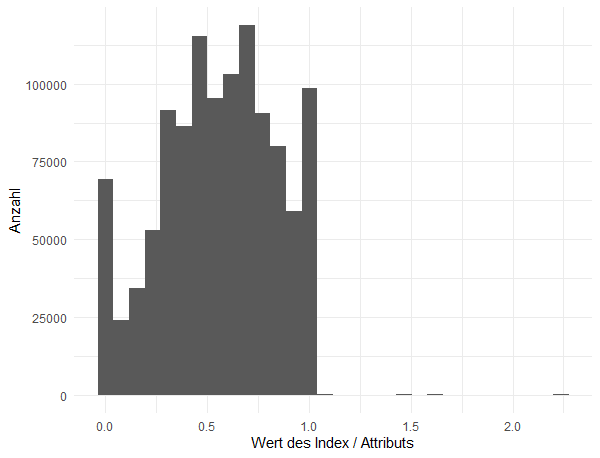
Histogramm aller Werte (alle Länder, Jahre und Attribute/Indizes)
Gut, dass wir das getan haben, denn wir erkennen eine nützliche Eigenschaft und erleben eine Überraschung: Die Werte liegen fast alle zwischen Null (Attribut ist abwesend) und Eins (Attribut ist vollständig anwesend). Das ist praktisch, denn so müssen wir später kein „feature scaling“ betreiben. Es gibt jedoch auch einige wenige Werte, die größer als Eins sind. Die schauen wir uns genauer an:
t_stacked %>% filter(values > 1)
Es handelt sich hier ausschließlich um den Index v_52_01 „Electoral participation“ (Wahlbeteiligung) und auch nur zu einigen Ländern und Jahren. Im „Codebook“ findet sich dazu folgende Klarstellung (ich übersetze sinngemäß):
Die Werte für die Bevölkerung im Wahlalter kann Unregelmäßigkeiten wie Probleme mit dem Wählerverzeichnis oder dem Registrierungssystem widerspiegeln. Diese Werte beruhen auf Schätzungen, da sie keine rechtlichen oder systemischen Hindernisse berücksichtigen oder nicht anspruchsberechtigte Mitglieder der Bevölkerung berücksichtigen. Daher kann dieser Index den Wert von 1 überschreiten, was kein Fehler ist, sondern solche Bedingungen widerspiegelt.
Gegebenenfalls müssen wir also Einträge dieses Index gesondert betrachten. Erlaubt sei dieser Hinweis: Daten vor der Analyse zu erkunden und gegebenenfalls zu säubern ist ein wesentlicher und oft zeitraubender Bestandteil der Arbeit. Ohne Skripte ist das gerade bei großen Datensätzen wie dem hier vorliegenden so mühsam, dass es im Zweifel sogar unmöglich wird.
Alles hängt miteinander zusammen
Als nächstes möchte ich verstehen, wie stark die vielen Indizes und Attribute untereinander korrelieren. Dafür wähle ich die Index- und Attributspalten aus, die praktischerweise mit „v_“ und „C_“ beginnen, bereite das Ergebnis als Matrix auf und verwende die Funktion rcorr(), die sowohl den Korrelationskoeffizienten als auch den dazugehörigen P-Wert bereitstellt. Bis auf wenige Ausnahmen sind alle unten dargestellten Korrelationen statistisch signifikant:
# Korrelationsmatrix erstellen:
corr.m <- t %>%
select(starts_with(c("v_", "C_"))) %>%
as.matrix() %>%
Hmisc::rcorr()
# Korrelationsmatrix graphisch aufbereiten:
gplots::heatmap.2(corr.m$r^2,
dendrogram = "none",
Rowv = FALSE, Colv = FALSE, trace = "none")
Zusammen mit einigen zusätzlichen Formatanweisungen für die heatmap.2 erhalten wir folgende Darstellung:
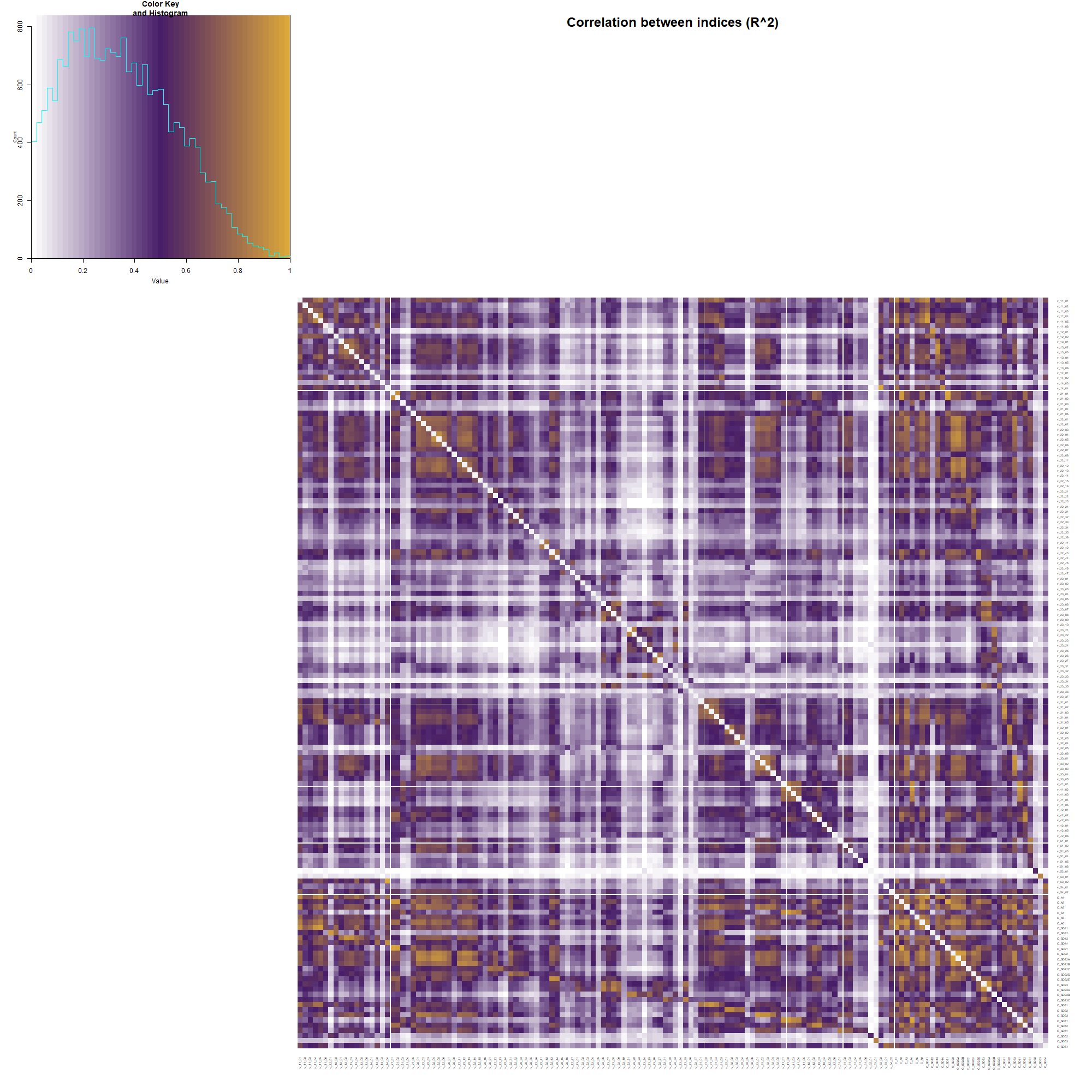
Korrelationen zwischen Attributen und Indizes, gemessen in R^2. Rechts unten befinden sich die aggregierten Attribute
Ich zeige hier R^2 anstatt des sonst üblichen Korrelationskoeffizienten R und behalte das Vorzeichen bei. Die statistische Größe R^2 hat eine anschauliche Bedeutung: ein R^2 von 90% bedeutet, dass die Variation eines Index zu 90% mit der Variation in eines anderen zusammenfällt („wenn der eine raufgeht, dann geht der andere auch rauf“). Nur 10% der Variation sind unabhängig. Wir erkennen starke Korrelationen auch weitab der Diagonalen: selbst Indizes, die zu anderen Hauptattributen gehören, gehen Hand in Hand. So korreliert zum Beispiel die Meinungsfreiheit (v_22_01 .. 08, Bestandteil der fundamentalen Rechte) mit einem effektiven Parlament (v_31_01 .. 05, Bestandteil der Überprüfung der Regierung).
Solche Einsichten mögen Dich nicht überraschen. Aber Hand auf’s Herz: hättest Du das vorhergesagt? Und alle die Korrelationen anderen auch? Dank der Daten können wir diese Muster nicht nur aufdecken sondern auch quantifizieren.
Um diesen Dingen weiter auf den Grund zu gehen, sortiere ich die so erhaltenen Daten nach R^2. Dabei stoße ich auf eine weitere Überraschung: Die Werte der Indizes v_14_04 (Wahlen) und v_53_02 (Direkte Demokratie) sind identisch (R^2 = 100%). Wir erkennen auch eine hohe Korrelation zwischen v_11_01 (Unabhängigkeit des Wahlleitungsorgans) und v_31_04 (Legislative Oppositionsparteien). Es dürfte schwer sein, in diesem großen Datensatz solche Zusammenhänge mit „Klicksoftware“ zu finden. Sobald sie jedoch gefunden sind, kannst Du sie auch mit Excel darstellen:
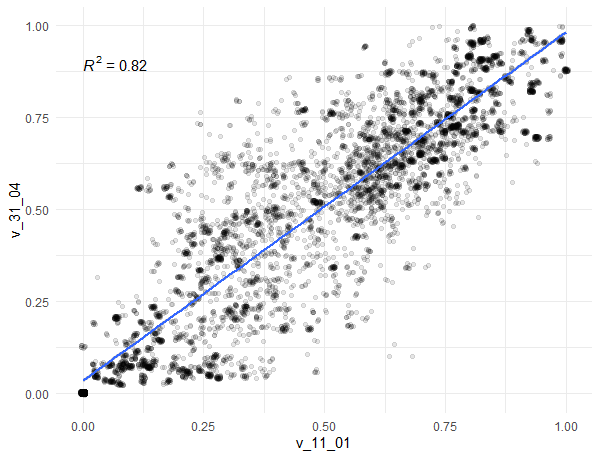
Zusammenhang zwischen v_11_01 (Unabhängigkeit des Wahlleitungsorgans) und v_31_04 (Legislative Oppositionsparteien). Dank der Transparenz der Punkte entsprechen Schwärzungen einer Häufung von Wertepaaren.
Unser Datensatz mit 116 gemessenen Merkmalen („Indizes“) hat etwa 15-20 Dimensionen
Bei starken Korrelationen in einem Datensatz sollten wir eine Hauptkomponentenanalyse durchführen: Hier haben wir es mit 116 Indizes v_ij_kl zu tun. Wenn diese unabhängig wären, dann hätte unser Datensatz 116 „Dimensionen“. Über eine Hauptkomponentenanalyse erfahren wir, wie viele „Dimensionen“ der Datensatz tatsächlich hat.
Dafür erstelle ich einen Arbeitsdatensatz der Indizes (die mit „v_“ beginnen), aus dem ich alle Zeilen mit NA-Einträgen herauslösche. Damit berechne ich die Hauptkomponenten PC und deren kumulierte Varianz, die ich graphisch als „Scree Plot“ darstelle:
workdata <- t %>%
select(starts_with(c("v_"))) %>%
drop_na
pca_obj <- prcomp(workdata)
data.frame(Var = pca_obj$sdev^2) %>%
mutate(PC = 1:length(pca_obj$sdev),
VarExplained = cumsum(Var)/sum(Var)) %>%
ggplot() +
geom_line(aes(x = PC,
y=VarExplained))
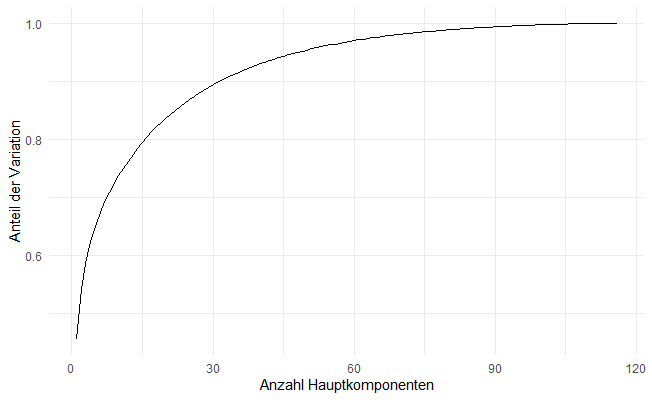
Hauptkomponentenanalyse: Kumulierte Variation gegen Anzahl der berücksichtigten Hauptkomponenten.
Die ersten 15 Hauptkomponenten erklären also etwa 80% (0.8) der beobachteten Variation. In anderen Worten: unser Datensatz mit 116 Spalten hat „im Großen und Ganzen“ 15 Dimensionen. Allein mit den ersten zwei Hauptkomponenten können wir sogar schon etwa 50% der Variation erklären.
Das ist eine nützliche Eigenschaft: Versuchsweise trenne ich meinen Arbeits- in einen Trainings- und einen Validierungsdatensatz und trainiere ein SVM-Modell (Support Vector Machine), mit dem ich die Regierungsformen im Validierungsdatensatz vorherzusage. Das Ergebnis sieht wie folgt aus:
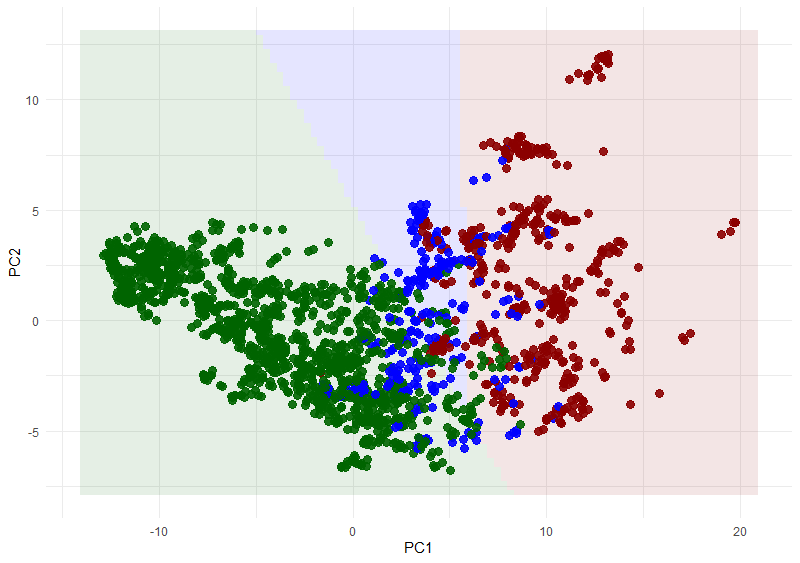
Vorhersage der Regierungsformen auf Grundlage der ersten zwei Hauptkomponenten. Punkte: „tatsächliche“ Regierungsform. Einfärbung: Modell. Grün: Demokratie, Blau: Hybrid. Rot: autoritäres Regime. Bei einem perfekten Modell lägen alle Punkte in dem Bereich der jeweiligen Farbe.
Wir erkennen, dass Demokratien und autoritäre Regime recht gut getrennt werden, hybride Regime sich jedoch auf Grundlage der beiden Hauptkomponenten nicht gut identifizieren lassen.
Entscheidungsbäume: worin unterscheiden sich die Regierungsformen?
Gehen wir ans Eingemachte: Wir haben mehr als hundert verschiedene Attribute und Indizes zu allen Ländern und Jahren, magst Du Dir sagen. Aber worin unterscheiden sich die Regierungsformen nun „wirklich“?
Unter den Hauptkomponenten können wir uns wenig vorstellen. Auch kann eine Regierung nicht einfach auf die ersten 3-5 Hauptkomponenten achten. Mit den Begrifflichkeiten des maschinellen Lernens formuliert: „feature extraction“ hilft uns hier nicht. Wir wollen die wesentlichen Merkmale auswählen können – „feature selection„.
Dieser Frage gehen wir auf Grundlage der „Indizes“ (v_ij_kl) nach und führen sie gemeinsam mit dem Ländernamen und der Regierungsform in einer neuen Arbeitstabelle („workdata“) zusammen. So erhalten wir mehr als 7000 Zeilen und bilden bei dieser Größe aus einem Fünftel einen Trainingsdatensatz („train“). Das Ergebnis validieren wir mit den verbleibenden Zeilen („valid“).
workdata <- t %>%
select(ID_country_name,
regime_status_name,
starts_with(c("v_")))
trainsize <- round(nrow(workdata)*0.2, 0)
trainvector <- sample(1:nrow(workdata), trainsize)
train <- workdata[trainvector, ] %>% select(-ID_country_name)
valid <- workdata[-trainvector, ] %>% select(-ID_country_name)
Wir erstellen nun eine Entscheidungsbaum-Klassifikation:
library(rpart)
library(rpart.plot)
classifier <- rpart(formula = regime_status_name ~ .,
data = train,
control = rpart.control(minsplit=10,
cp=0.1))
rpart.plot(classifier, type = 1, cex = 0.8)
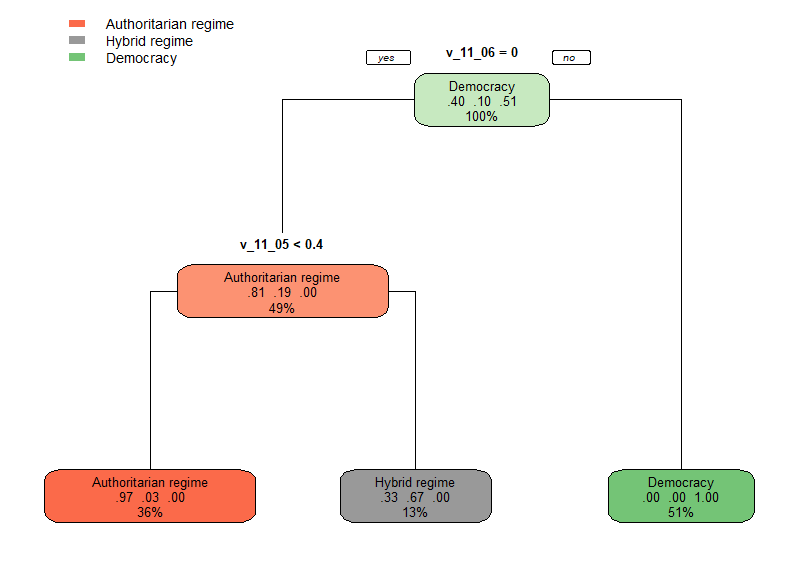
Entscheidungsbaum für Regierungsformen.
Demokratien können wir also sehr gut daran erkennen, dass es bei Wahlen einen echten Wettbewerb gibt (v_11_06). Wenn wir dieses Kriterium anwenden, dann verfängt sich in den Validerungsdaten nicht ein einziges autoritäres oder hybrides Regime.
Die Unterscheidung zwischen autoritären und hybriden Regimen entscheidet sich anhand von freien und fairen Wahlen (v_11_05). Allerdings ist diese Aufteilung nicht besonders genau: immerhin wird ein Drittel (0.33) der hybriden Regime fälschlicherweise als autoritär klassifiziert. Wir erhalten also ein ähnliches Bild wie bei der SVM-Modellierung über die beiden ersten Hauptkomponenten:
Hybride Regierungsformen scheinen ein schwer greifbares „Zwischending“ zu sein.
Unser Glas ist dennoch deutlich mehr als halbvoll: Insgesamt werden immerhin 94% aller Regierungsformen richtig klassifiziert, wie wir feststellen, indem wir den Entscheidungsbaum verwenden, um die Regierungsform in dem Validierungsdatensatz vorherzusagen, und dieses Ergebnis mit den „echten“ Werten vergleichen.
Wir verstehen 94% von dem was los ist!
Da ich für diese Betrachtungen einen zufälligen und absichtlich kleinen Trainingsdatensatz gezogen habe, wiederhole ich meine Analyse einige Male und stelle fest, dass der Algorithmus für manche Stichproben anstatt v_11_05 < 0.4 den Index v_13_02 < 0.7 („Hürden für Parteien“) heranzieht. Wir halten fest:
Laut unseren Daten zeichnen sich Demokratien vor allem durch freie und faire Wahlen aus, bei denen ein echter Wettbewerb zwischen Parteien stattfindet.
Auch das mag nicht überraschend sein und nach dem Merksatz eines Schulbuchs aus der 11. Klasse klingen. Wir erleben hier etwas, das ich auch bei der Analyse von Unternehmensdaten immer wieder sehe: Zunächst stößt Du auf bekannte oder zumindest wenig überraschende Zusammenhänge, die Leute vom Fach schon kennen. Aber wieder Hand auf’s Herz: Hättest Du die Eingangsfrage auch so beantwortet? Und auch wenn Du es getan hast: ist es nicht gut, hier schwarz auf weiß eine Bestätigung durch Daten vorliegen zu haben?
Zu dieser nicht ungewöhnlichen Situation möchte ich Dir folgendes mitgeben:
- Dank einer Datenanalyse braucht es nicht jahrelange Erfahrung, um Einsichten zu gewinnen.
- Du kannst mit einer Datenanalyse nicht nur Zusammenhänge und Muster erkennen. Du kannst auch ihre Stärke quantifizieren.
- Es besteht ein großer Unterschied zwischen „ja, ja, das ist nichts Neues“ und einer auf Datengrundlage erzeugten Liste von Einsichten.
Ich hoffe, diese drei Punkte helfen Dir bei Deiner Arbeit als Analyst oder Analystin. Denn wenn Du Dein Vorgehen von Anfang an richtig kommunizierst und darauf hinweist, dass Du vermutlich zunächst bekannte Zusammenhänge finden wirst (frage gerne vorher nach, welche Zusammenhänge Dein Publikum erwartet), dann schaffst Du Vertrauen in Deine auf Datenbasis gewonnen Aussagen. Neue und manchmal „schwer verdauliche“ Einsichten kommen später – und für die brauchst Du eben dieses Vertrauen.
Das Ende der Fahnenstange: können wir die Regimeformen überhaupt anhand der vorliegenden Daten unterscheiden?
Nach unseren Erfahrungen mit den Hauptkomponenten und den Entscheidungsbäumen liegt die Frage nahe: lohnen sich weitere Untersuchungen überhaupt – oder hat jemand die zu einem Datensatz gehörige Regimeform „geschätzt“ oder gar „gewürfelt“?
Bevor wir uns allzu sehr plagen, packe ich gleich die ganz große Bazooka aus: Neuronale Netze. Die gibt’s andernorts nur gegen den branchenüblichen Aufpreis der Bezahlsoftware. Mit R und Python hast Du das „für umme“: Mit wenigen Zeilen kannst Du – solange Du eine Internetverbindung hast – neuronale Netze auf fernen Servern rechnen lassen.
Ich verwende h2o und baue ein neuronales Netz aus vier Ebenen mit je 60 Neuronen auf – der Fadenwurm hat 302. Die 60 Neuronen je Ebene entsprechen in etwa der Hälfte der Anzahl an Features v_ij_kl – meine Daumenregel für neuronale Netze. Trainings- und Validierungsdatensätze habe ich dabei wie oben erstellt:
library(h2o)
h2o.init(nthreads = -1)
classifier <-
h2o.deeplearning(y = 'regime_status_name',
training_frame = as.h2o(train),
activation = 'Rectifier',
hidden = c(60, 60, 60, 60),
epochs = 100,
train_samples_per_iteration = -2)
y_pred <- h2o.predict(classifier,
newdata = as.h2o(valid)) %>%
as.data.frame()
Das Ergebnis ist – gelinde gesagt – der Hammer. Falls Du selbst versucht hast, den Regime-Status anhand der Indizes vorherzusagen, dann kannst Du das vermutlich nachvollziehen. Hier ist die „Confusion Matrix“:
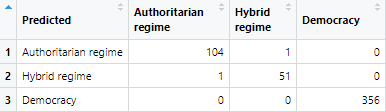
Confusion Matrix des mit neuronalen Netzen erhaltenen Modells: nur zwei Ereignisse wurden falsch klassifiziert.
Die Aussage lautet:
„Gib mir einen vollständigen Satz an Indizes v_ij_kl zu einem x-beliebigen Land. Ich kann Dir dann mit 99,9%-iger Sicherheit sagen, um welche Regimeform es sich handelt“.
Wenn Du ein wenig Erfahrung mit Wertungsdaten („judgemental data„) wie diesen hast, dann wirst Du jetzt vermutlich auch tief durchatmen:
„Die Leute von State of Democracy haben wirklich sehr, sehr saubere Arbeit geleistet!“
Um es ganz klar zu sagen: fake data sehen anders aus. Wir haben es mit einem Datensatz von sehr hoher Qualität zu tun.
Der Vollständigkeit halber wiederhole ich diese Analyse mit einem Random Forest und mit allen Attributen, Sub- und Subsub-Attributen und Indizes. So stoße ich auf ein ähnlich gutes Ergebnis: Wir müssen also gar nicht einmal die künstliche neuronale Intelligenz bemühen. Eine Vielzahl von Entscheidungsbäumen, der „Zufallswald“, führt ebenfalls zum Ziel.
Gleichzeitig hilft’s aber auch nichts, denn unsere Frage lautet: welche Indizes („feature selection„) sagen denn die Regierungsform am besten vorher? Wenn Du ein Land regierst, dann hast Du die auch aus dem Unternehmensalltag bekannte Frage:
„Ich kann doch nicht einfach auf 116 Merkmale gleichzeitig achten. Sagt mir bitte, was wir priorisieren sollen!“
Hier sind wir eine Antwort schuldig. Ich tue folgendes – und erspare Dir die Details: Zunächst rechne ich eine ordinal-logistische Regression der Regierungsform gegen alle 116 Indizes und sortiere das Ergebnis algorithmisch nach der Größe der Koeffizienten. Mit den 20 größten starte ich eine neue logistische Regression und entferne Schritt für Schritt die Indizes mit den kleinsten Koeffizienten, wobei ich jeweils die Confusion Matrix im Blick behalte. Das dauert vertretbare 15 Minuten. Vielleicht gibt es auch eine „best-subset“ Lösung in R für die ordinal-logistische Regression. Die habe ich nicht gefunden und musste also zu Fuß ran.
Aber dann, oh Wunder: am Ende stoße ich erneut auf die gleichen drei Indizes wie auch schon beim Entscheidungsbaum. Die Genauigkeit meines so erhaltenen Modells liegt bei 96%, etwas mehr als die 94% vorher, was kein großer Gewinn und vermutlich nicht einmal signifikant ist.
Das Glas ist dennoch mehr als halb voll, denn unsere wesentliche Einsicht besteht darin, dass wir jetzt auf zwei Wegen die gleiche Aussage gefunden haben:
Demokratien zeichnen sich vor allem durch freie und faire Wahlen aus, bei denen ein echter Wettbewerb zwischen Parteien stattfindet.
Können wir einen Regimewechsel vorhersagen?
Eine durchaus brisante Frage …
Vielleicht ist Dir die bisherige Diskussion recht abstrakt vorgekommen. Denn wir haben versucht, die Regierungsformen über einen Minimalsatz an Indizes zu definieren. Geradezu brisant erscheint jedoch folgende Frage:
Können wir einen Regimewechsel vorhersagen?
Das hätte durchaus praktische Konsequenzen: So könnten wir eine Art „Frühwarnsystem“ einrichten, über das die Vereinten Nationen, die Weltbank oder wer auch immer Länder erkennen, die es zu unterstützen gilt.
… für die wir Muster in einem „Kuddelmuddel“ erkennen müssen
Zunächst einmal wollen wir Regimewechsel überhaupt sichtbar machen. Dafür bilden wir einen neuen Arbeitsdatensatz, fügen eine Spalte ein mit dem Regime-Status des Vorjahres („lag“) und betrachten lediglich die Änderungen:
wd <- t %>%
select(ID_country_name,
ID_year,
regime_status_name,
democratic_performance_name)
wd$Lag <- lag(wd$regime_status_name)
# Hier wechselt ein Land. Das wollen wir ausschließen:
wd$Lag[wd$ID_country_name != lag(wd$ID_country_name)] <- NA
wd$change <- ifelse(
wd$regime_status_name == wd$Lag,
"Stable",
paste(wd$Lag,
wd$regime_status_name,
sep = " to "))
ggplot(data = wd %>%
filter(change != "Stable"),
aes(x = ID_year,
fill = change)) +
geom_bar()
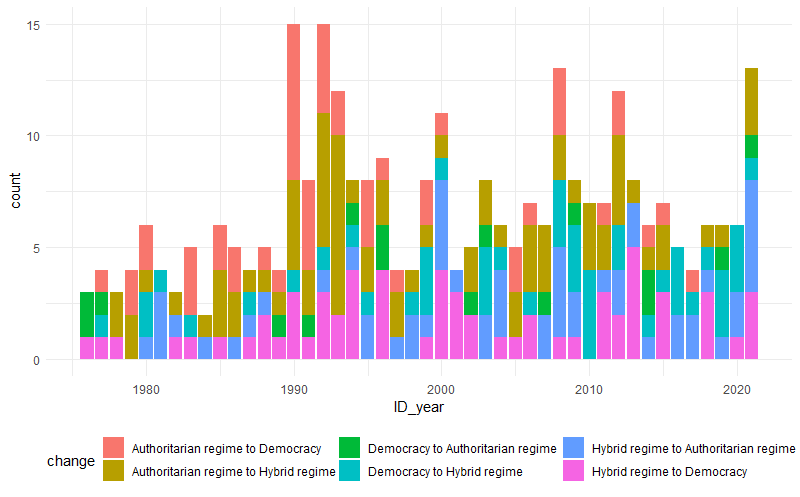
Anzahl der Regimeänderungen im Laufe der Zeit.
Solche Graphiken findest Du im Unternehmensalltag häufig. Von „Data Journalists“ – diesen Beruf gibt es – wirst Du das nicht finden und ich zeige dieses Ergebnis hier als abschreckendes Beispiel:
Siehst Du auch, was ich hier sehe?
Nichts! Solche Graphiken gehören nicht gezeigt. Um Aussagen zu treffen, müssen wir die Daten besser aufbereiten.
Regimewechsel häufen sich zu bestimmten Zeiten
Wir fragen deshalb präziser: gibt es Phasen, in denen sich ein bestimmter Regimewechsel häuft? Das können wir sehr gut mit Regelkarten beantworten und bereiten die Daten entsprechend auf:
tab <- table(wd$ID_year, wd$change) %>%
as.data.frame() %>%
pivot_wider(names_from = Var2,
values_from = Freq)
tab$Total <- rowSums(tab[, 2:ncol(tab)])
tab <- tab[-1, ]
Aus dieser Tabelle tab können wir nun Spalte für Spalte alle Regime-Änderungen auswählen und darstellen, zum Beispiel die zweite:
library(qcc)
col <- 2 # Wir wählen 2..7 für die Regime-Änderungen
p_chart <- with(tab,
qcc(tab[, col] %>% pull(),
tab$Total,
type = "p",
data.name = colnames(tab)[col],
labels = tab$Var1))
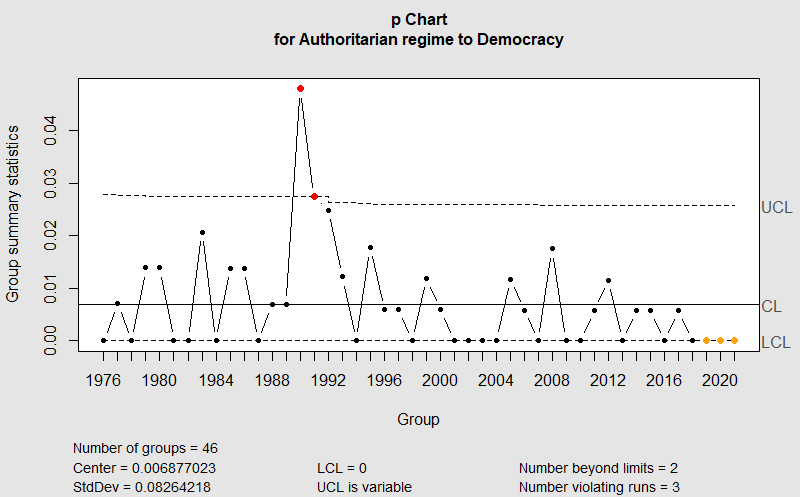
Regelkarte für die Rate der Änderungen „Autoritäres Regime zu Demokratie“. Anfang der 1990er Jahre sehen wir viele derartige Regimewechsel.
Wenn Du aus meiner Generation kommst, dann verstehst Du diese Graphik sofort: Ende der 1980er Jahre wehten die „Winds of Change“ über die Welt. Ein erstaunlich großer Anteil von autoritären Regimen wurde „über Nacht“ demokratisch.
Indem wir die Spaltenzahl (col = 2) in obigem Skript ändern, finden wir folgende Ergebnisse:
- Autoritär zu Demokratie: sehr viel 1990/91; sehr wenig 2019/20/21
- Autoritär zu Hybrid: sehr viel 1992/93 (also leicht zeitversetzt)
- Demokratie zu autoritär: ohne Befund; stabil bei ca. 0,2% p.a.
- Demokratie zu hybrid: ohne Befund; stabil bei ca. 0,6% p.a.
- Hybrid zu autoritär: wenig 1988-1994; viel 2021
- Hybrid zu Demokratie: wenig vor 1988.
Vorhersage von Regimewechseln
Für diese Aufgabe gehen wir „all in“ und setzen alle Indizes und Attribute ein, über die wir verfügen. Aus der Spalte für den Regimewechsel berechnen wir eine neue Spalte „ChangeType“ für die Regimeform im folgenden Jahr:
- „Up“ für einen Wechsel von autoritär zu hybrid bzw. zu demokratisch und von hybrid zu demokratisch
- „Down“ für die umgekehrte Richtung, also hybrid zu autoritär und demokratisch zu hybrid bzw. autoritär
- „Stable“ für keine Änderung.
Über alle Länder und Jahre hinweg finden wir so bei 7107 stabilen Situationen 116 „Down“ und 193 „Up“ Änderungen, mit denen wir wieder ein Modell trainieren, um die Situation „Up“, „Down“ oder „Stable“ des Folgejahres zu berechnen. Dafür haben wir einen Arbeitsdatensatz erstellt aus allen „Up“ und „Down“ Änderungen und eine Stichprobe im Umfang von 154 (Mittelwert aus 116 und 193) der „Stable“-Situationen – denn sonst würden wir das Modell vor allem für stabile Situationen trainieren, wo wir uns jedoch für die Änderungen interessieren. So trainieren wir mit 370 Datensätzen und validieren mit 93 Datensätzen. Beide Datensätze haben 148 „feature„-Spalten.
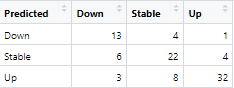
Confusion Matrix für die Vorhersage einer Regimeänderung. Klassifizierung mit einem neuronalen Netz.
„Down“-Änderungen wurden also in 13 Fällen richtig erkannt, in 6 Fällen fälschlicherweise als „stabil“ und 3 mal sogar als „up“ vorhergesagt. „Down“ Änderungen werden demnach in ca. 60% der Fälle richtig erkannt. Ähnlich sieht es bei den stabilen Situationen aus (64%). „Up“ wurde in immerhin 86% der Fälle richtig erkannt, was statistisch mit einem P-Wert von 3% auch signifikant besser ist.
In dem Versuch, das Ergebnis zu verbessern, führt auch ein Random Forest nicht weiter: da in den Prädiktoren keine NA-Werte erlaubt sind, haben wir somit nur eine kleine Datenbasis. Ich habe auch folgendes (rechenintensive) Experiment angestellt: vielleicht spielt ja nicht nur der Status im Vorjahr eine Rolle sondern die Entwicklung über mehrere Jahre hinweg von Indizes und Attributen? Also habe ich Spalten berechnet für die Trends der jeweils letzten fünf Jahre und dabei nur statistisch signifikante Trends vermerkt. Das neuronale Netz wird dadurch unwesentlich besser: Aufwand und Nutzen stehen in keinem vertretbaren Verhältnis.
Was sagt das Modell für 2022 voraus?
Auch wenn ich über die Güte des Modells nicht glücklich bin, so können wir es dennoch verwenden, um aus dem letzten verfügbaren Stand des Jahres 2021 Vorhersagen für das Jahr 2022 zu treffen:
y2021 <- wd %>% filter(ID_year == 2021)
pred_2022 <- h2o.predict(classifier, newdata = as.h2o(y2021))
So finden wir 20 Bewegungen „up“ und 36 „down“. Die Ergebnisse möchte ich hier nicht teilen, weil ich meine Klassifikation nicht für gut genug halte, um zu zeigen, was zum Beispiel für Indien, Russland, Singapur oder die Ukraine vorhergesagt wird. Natürlich: wenn ich die Ergebnisse anschaue, dann sage ich: „Klar, das ist tatsächlich auch so gekommen“. Diese Lektion haben wir aber oben schon gelernt: Wenn wir hinterher so schlau sein wollen, dann müssen wir vorher unsere eigene Vorhersage aufschreiben…
Könnten wir das Modell nicht noch verbessern?
Ja, das könnten wir bestimmt. Ich habe mir einige Regimewechsel im Democralyser angeschaut. Es scheint bestimmte Muster zu geben, die Fachleute vermutlich längst kennen. Deren Verständnis, zu Trends oder Wechselwirkungen zum Beispiel, könnte man in zusätzlichen Spalten festhalten. Oder aber man verzichtet auf gewisse Spalten und versucht es so – auch mit anderen Ansätzen, denn neuronale Netze sind auch nicht immer der Weisheit letzter Schluss. Hier fängt eben die „echte“ Arbeit an. Wie heißt es so schön bei Michael Ende:
Aber das ist eine andere Geschichte.
Und die soll ein andermal erzählt werden.
Was Du mitnehmen kannst
Am wichtigsten ist mir, dass Du einen Eindruck davon mitnimmst, wie vielfältig verschiedene Länder ihre Regierungsform gestalten und auf was es Menschen dabei ankommt. Wenn Du die fünf Hauptattribute jetzt aufzählen kannst, dann habe ich viel erreicht. Du weißt jetzt auch, dass Dir sehr gute Daten vorliegen, die Du mit dem Democralyser selbst erkunden kannst.
Mir liegt auch die Datenanalyse am Herzen und ich glaube, auch Du solltest Dich damit auseinandersetzen. Dabei geht es mir zum einen um das Coden. Zum anderen aber auch um die Verwendung von statistischen Werkzeugen und die gebotene Sorgfalt bei der graphischen Darstellung. Wie wir hier gesehen haben sind Regelkarten nicht nur im Qualitätsmanagement oder bei der Steuerung von Produktionsprozessen sinnvoll.
Du hast auch anhand eines praktischen Beispiels gesehen, dass eine hohe Modellgüte zwar wünschenswert ist – ein neuronales Netz erreicht 99,9% für die Klassifikation der Regierungsform anhand der Indizes. Wir ihm aber nicht über die Schulter schauen. Auch „feature extraction“ ist wenig anschaulich. So kommt „best subset“-Analysen eine wichtige Rolle zu.
Ich bin mir auch sicher, dass echte Experten und Expertinnen hier noch mehr herausgeholt hätten und vielleicht auch Nachlässigkeiten oder gar Fehler finden werden. In dem Fall bitte ich um Hinweise – und mache jetzt Frühstück für die Familie.