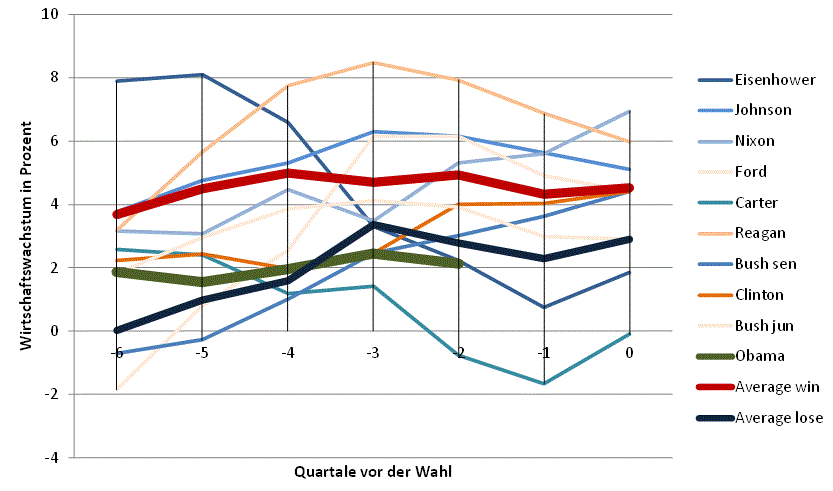
Der Economist hat am 13. Oktober 2012 eine (externer Link) Graphik veröffentlicht, um Daten zur Beantwortung dieser Frage heranzuziehen. Bitte nehmen Sie sich die Zeit und schauen Sie sich diese Daten an. Vermutlich werden auch Sie die Augen zusammen kneifen müssen, um die Aussage des Economist herauszulesen: die Wirtschaftsdaten legen eine Wahlniederlage Obamas nahe.
Davon abgesehen: der Economist formuliert die Problemstellung sehr geschickt: welche Faktoren könnten bestimmen, ob der aktuelle Präsident (so er denn kandidiert) wieder- oder abgewählt wird? So gefragt kann man Daten sammeln und analysieren.
Ihnen fallen sicher sofort „Wirtschaftswachstum“, „Arbeitslosenquote“, „Inflationsrate“ ,
„Kosten der Wahlkampagne“ und ähnliches ein. Wir wollen nicht spekulieren, und
sie einfach in einem (externer Link) Ishikawa-Diagramm strukturiert aufzählen. Die Krux dabei ist jedoch folgende: je mehr dieser möglichen Einflussfaktoren Sie auf Signifikanz testen wollen, desto mehr Daten brauchen Sie: zwei Punkte für eine Gerade, drei spannen eine Ebene auf – und so weiter. Sie müssen schließlich auch ein paar Punkte „übrig haben“, um zu testen, ob alles stimmig ist. (Wem sich bei dieser Beschreibung einer Regressionsanalyse die Nackenhaare sträuben, der weiß mehr als ich hier voraus setzen möchte).
Der Economist geht sehr vorsichtig an die Sache heran:
1) Er zieht lediglich die Wahlergebnisse nach dem II. Weltkrieg heran: es könnte ja sein, dass sonst „Äpfel mit Birnen verglichen“ würden.
2) Er testet lediglich einen Faktor, das wirtschaftliche Wachstum (in einer getrennten Graphik auch die Arbeitslosenquote) – und zwar für die letzten 6 Monate vor der Wahl.
Die sodann präsentierte (externer Link) Graphik stellt das Wirtschaftswachstum Quartal für Quartal vor Präsidentschaftswahlen dar, die entweder gewonnen (hellblau) oder verloren (rosa) wurden. Die Chancen von Obama werden eher schlechter bewertet, da seine Kurve in der Nähe des Mittelwerts der historischen Wahlverlierer liegt (blaue Kurve).
Aus Sicht einer Statistikerin stellt das aber lediglich die Formulierung einer Hypothese dar: die Daten könnten nahe legen, dass Obama verliert. Wie groß seine Gewinnchancen tatsächlich sind, das lässt sich so nicht ermitteln.
Die hier betrachtete Problemstellung ist ein Beispiel für „kontinuierliches x“ (das
Wirtschaftswachstum kann ein Kontinuum von Werten annehmen) gegen ein
„diskretes Y“ (die Wahl wird entweder gewonnen oder verloren). Gesucht ist Y =
f(x). Berühmt geworden ist die dahinter stehende (externer Link) „Logistische Regression“ über die (externer Link) Challenger-Katastrophe 1986: dem NASA-Team lagen Daten zwar vor zur Brüchigkeit von Dichtungsringen („gebrochen, nicht gebrochen“) in Abhängigkeit von der Temperatur. Diese Daten konnten aber nur unzulänglich interpretiert werden – mit fatalen Folgen.
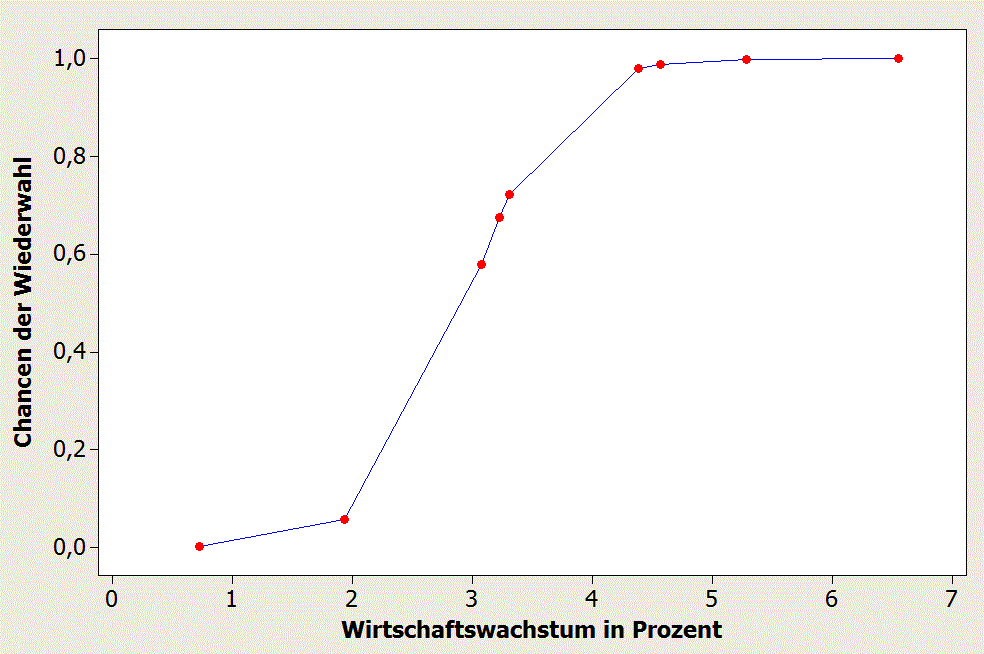
Die oben vom Economist zitierten Daten habe ich mittels logistischer Regression ausgewertet. Weder der Trend des Wirtschaftswachstums noch der Wert eines bestimmten Quartals spielen (bei 95% Signifikanz) eine Rolle. Zieht man jedoch den
Mittelwert des Wirtschaftswachstums der letzten 6 Quartale heran, dann ergibt
sich ein „(externer Link) P-Wert“ von 0,009. In anderen Worten: mit 99.1% Wahrscheinlichkeit ist die so aufgedeckte Korrelation von Wirtschaftswachstum zu Wiederwahl kein „Zufallsprodukt“.
Die logistische Regression erlaubt zudem, eine Vorhersage-Gleichung abzuleiten. So ergibt sich folgende Kurve:
Für Barack Obama liegen bisher nur die Wirtschaftsdaten der Quartale 6..2 vor der Wahl vor. Der Durchschnitt aus diesen liegt bei zwei Prozent. Ups…
Was (im Gegensatz zur „gewöhnlichen“) die logistische Regression nicht zulässt ist, einen R^2-Wert zu bestimmen. Dieser besagt, wie viel der beobachteten Variation in Y sich über eine Variation in x erklären lässt. Konkret hier: wie viel Spielraum lässt der beobachtete Zusammenhang anderen Faktoren als nur dem Wirtschaftswachstum? Angemerkt sei, dass die logistische Regression solche Faktoren durchaus mit einbeziehen kann, also Y = f(x1, x2, …).
Zurück zur Aussage des Diagramms. Wenn ich diese Dinge hier schreibe, dann nicht, weil etwa diese statistische Beurteilung meinem Wunsch oder meiner Abneigung
entspräche. Einer der besten politischen Prognostiker, (externer Link) Nate Silver, sagt zudem das Gegenteil des Schlusses voraus, den wir hier ziehen. Es geht mir einzig darum: wir wollen Zahlen die in ihnen steckenden Botschaften entlocken. Wir können dafür im Kaffeesatz einiger Excel-Graphiken rühren. Oder wir verwenden das quantitative Werkzeuge. Es kann in der Tat gelegentlich sehr wichtig sein, so seine Schlüsse zu ziehen.
Mein „Kochrezept“ zur Datenanalyse lautet deshalb:
1) Graphische Analyse, um so viele Hypothesen zu formulieren wie möglich
2) Statistische Analyse, um diese zu prüfen
3) Erneute graphische Darstellung, in der nur noch signifikante Signale vorkommen
4) Diese Darstellungen verwenden, um Veränderung zu initiieren.