Sparen ist angesagt
Seit Monaten wird darüber gesprochen, dass im jetzt kommenden Winter ein Energieproblem auf Deutschland zukommen wird oder kann – je nach dem, was man als „Problem“ betrachtet und wem man zuhört. Es scheint eine relativ einhellige Meinung darüber zu bestehen, dass wir unseren Energieverbrauch um ca. 20% reduzieren müssen, um das Risiko eines Blackouts zu reduzieren.
Wo steht mein Haushalt eigentlich?
Ein Blick in unsere Strom- und Gasabrechnungen der letzten Jahre zeigt, dass unser drei-Personen-Haushalt im Mittel der letzten Jahre pro Jahr
- ca. 10.000 kWh Gas und
- ca. 2.500 kWh Strom
verbraucht hat. Laut unserem Anbieter scheinen wir damit deutlich unter dem Durchschnitt zu liegen.
Messen einfach gemacht: Strom- und Gaszähler
Gerade für Strom gibt es allerhand Messgeräte, die man direkt vor den Verbraucher, z.B. den Fernseher, schalten und so die vom Gerät entnommene Leistung messen kann. Aber wie machen wir das für die Mikrowelle oder den E-Herd (den wir kaum benutzen)? Lohnt es sich also, so ein Gerät anschaffen? Und warum für Strom, wenn es für Gas nichts vergleichbares zu geben scheint (für den individuellen Verbrauch von Gasherd, -heizung und für Warmwasser)?
Wir haben deshalb beschlossen, einfach direkt an Strom- und Gaszähler abzulesen. Der Nachteil liegt auf der Hand: Rückschlüsse auf einzelne Verbraucher sind nicht ohne weiteres zu haben. Wieviel verbraucht zum Beispiel mein Computer im Laufe von 24 Stunden, wenn ich ihn nachts nicht ausschalte? Gleichzeitig können wir beliebig lange – und auch beliebig genaue Zeitreihen erfassen. Die sehen dann wie folgt aus:
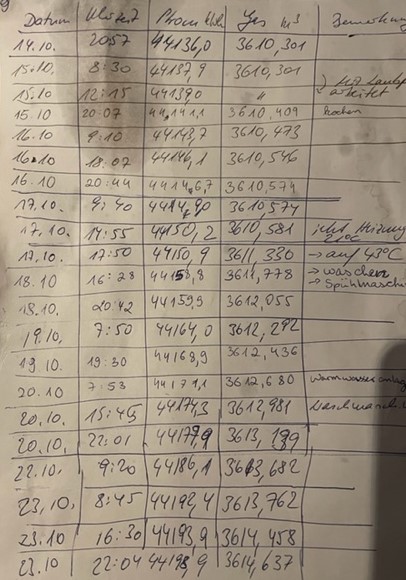
Wir erfassen also
- das Datum
- die Uhrzeit
- den Zählerstand Strom in Kilowatt-Stunden
- den Zählerstand Gas in Kubikmeter und
- „Bemerkungen“.
Dank der „Bemerkungen“ können wir – zumindest im Prinzip und falls wir „fleißig genug“ sind – zum Beispiel den Verbrauch der Waschmaschine erfassen, indem wir jeweils vor- und einem Waschgang den Strom ablesen.
Der Gaszähler zeigt Kubikmeter an – wir bezahlen aber Kilowattstunden!
Wenn man einmal anfängt, den Dingen auf den Grund zu gehen, dann erlebt man Überraschung: ablesen können wir am Gaszähler die Kubikmeter, wir bezahlen aber Kilowattstunden. Was die Umrechnung angeht, da vertrauen wir also dem Gaslieferanten (und dem zuständigen Eichamt).
In unserer Gasrechnung findet sich dazu eine sparsame Erklärung: der „Brennwert“, also wieviel Energie das Gas je Kubikmeter enthält, hängt von der Zusammensetzung des Gases ab. Im Internet erfahre ich, dass es auch eine „Zustandszahl“ gibt, die Temperatur und Druck berücksichtigt. Nun wird die Temperatur im Winter vermutlich geringer sein als im Sommer und der Kubikmeter Gas enthält dann auch mehr Energie. Welche Werte für welchen Zeitraum unserer Abrechnung zugrunde gelegt werden, darüber schweigt sich unsere Abrechnung aus. Im Internet finden sich einige interessante Referenzen, zum Beispiel auch diese hier. Man könne, so heißt es dort, den Abrechnungsbrennwert „regelmäßig“ beim Gaslieferanten erfragen.
Ein Anruf dort stößt tatsächlich auf Verständnis: „Ich finde gut, dass Sie nachfragen.“ Für unseren Wohnort wird uns ein Brennwert von 10,5 – 10,6 genannt und eine Zustandszahl von 0,976. Also rechne ich wie folgt um:
Verbrauchte Energie [kWh] = 10,6 * 0,976 * Verbrauchtes Gas [m^3]
Wir wollen unsere Freiheiten bei der Datenerfassung und -auswertung
Der Teufel steckt bekanntlich im Detail.
Das wird nach den ersten Tagen schon klar.
Ich habe unsere Daten in ein Excelblatt übertragen und möchte sie auswerten. Zur Analyse würde man sich wünschen, dass die Werte regelmäßig, zum Beispiel täglich um 08:00 Uhr, erfasst werden. So könnte man dann den Verbrauch innerhalb von 24 Stunden bestimmen und vergleichen. Diese Disziplin bringen wir als Familie jedoch nicht auf. Bei uns liegt vielmehr der oben abgebildete Zettel in der Küche und wer auch immer möchte kann kurz in den Hauswirtschaftsraum herübergehen und eine neue Zeile eintragen.
Ich habe deshalb beschlossen, die Daten stattdessen mit einem R-Skript auszuwerten. Da ich noch nicht genau weiß, welche Auswertungen ich im Laufe der Zeit erstellen möchte, bleibe ich so flexibel. Das Skript kann zudem im Laufe der Zeit in einen Markdown-Report übertragen werden und so würden dann alle Auswertungen „per Knopfdruck“ zur Verfügung stehen. Das Excel-Blatt dient dabei lediglich als „Datenbank“. Das Programm Power-BI wäre dazu eine mögliche Alternative.
Erste Auswertung: einfacher Zeitverlauf
Mein Skript liest zunächst die Rohdaten aus dem Excelblatt ein und ich überführe die Daten in eine „aufgeräumte Struktur“, sodass jeweils eine Spalte entsteht für:
- Datum und Uhrzeit
- Energieverbrauch in kWh
- Energieform (Gas oder Strom).
Dafür werden die Spalten jeweils „gestapelt“. Unter Verwendung des ggplot-Pakets in R lässt sich so mit folgenden Befehlszeilen (Formatierungsanweisungen habe ich der Einfachheit halber herausgenommen)
ggplot(data = plotdat,
aes(x = Datum,
y = kWh,
colour = Energie)) +
geom_line()
diese Graphik erstellen:
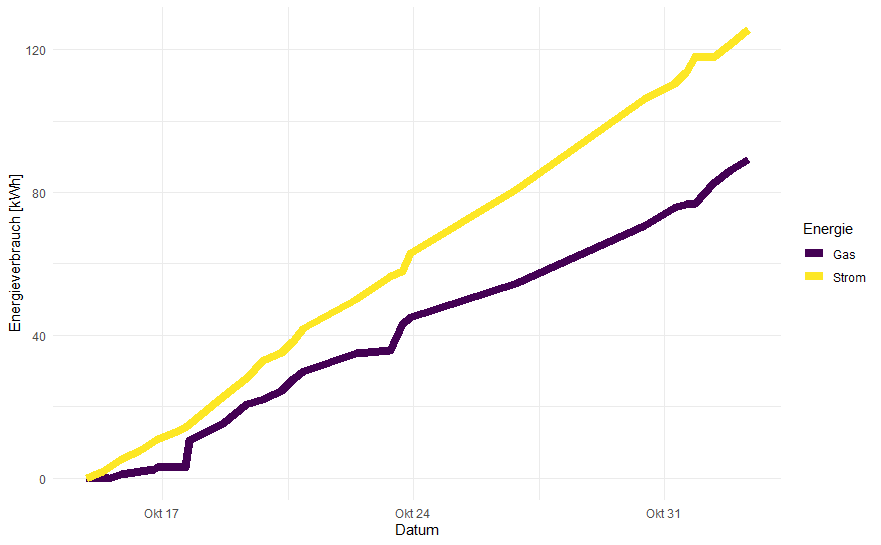
Im betrachteten Zeitraum erkennen wir zunächst einen ziemlich gleichmäßigen Verbrauch. Im Jahr 2022 war der Oktober sehr warm und wir haben bis Ende Oktober nicht (mit Gas) geheizt: tagsüber scheint die Sonne herein, abends ziehen wir die Vorhänge zu, um die Wärme im Haus zu behalten. Dank guter Isolierung hat das bisher gereicht. Ein Vergleich zu später wird also interessant werden.
Ganz zu Beginn unserer Messungen steht ein Experiment: wir haben für einige Tage das Gas vollständig aus- und nur dann kurz wieder eingeschaltet, wenn das Duschwasser zu kalt geworden ist. Das Ergebnis ist anhand des bis zum 18. Oktober deutlich flacheren Verlaufs des Gasverbrauchs zu erkennen.
Der durchschnittliche Verbrauch lässt sich nun über eine Regressionsanalyse ermitteln:
model <- lm(StromverbrauchkWh ~ DatumUhrzeit, data = t) summary(model)
So ergibt sich, dass (R-Quadrat) 99,9% der beobachteten Variation im Stromverbrauch mit dem Fortschreiten der Zeit zusammenhängen und nur 0,1% mit „Spezialeffekten“, wenn wir die Waschmaschine, einen Laubpuster oder den Trockner (kurz) laufen lassen. Der durchschnittliche tägliche Verbrauch lässt sich anhand der Steigung ermitteln. Wir erhalten:
- Gas: 4,9 kWh/24h (R^2 = 99,1%)
- Strom: 6,9 kWh/24h (R^2 = 99,9%)
Mit Blick auf das nun angekündigte kühlere Wetter – und wir haben heute die Heizung von „Schutzbetrieb“ auf „Eco“ umgeschaltet – liegt jedoch folgender Wunsch nahe: Wir wollen diese Regressionsanalyse nicht einfach nur über den gesamten Betrachtungszeitraum durchführen. Das wäre ohne weiteres auch in Excel möglich. Vielmehr möchten wir in der Lage sein, über ein wählbares Zeitfenster, zum Beispiel über 7 Tage hinweg, solch eine Regression durchzuführen, um die dadurch entstehende Zeitreihe untersuchen zu können. Schwankungen im durchschnittlichen Verbrauch sollten so erkennbar sein.
Bei diesem – relativ einfachen – Wunsch steigen meinem Kenntnisstand nach jedoch Excel, Power-BI und jegliche „Klick-Software“ aus – es sei denn, man erstellt ein Skript. Genau das tun wir von Anfang an in R.
Das Ergebnis wollen wir uns beim nächsten Mal anschauen.