Es ist einige Zeit vergangen seit meinem letzten Blogeintrag.
Ein Nachtrag
Kurz zum letzten Eintrag: Es zeichnet sich inzwischen eine Entwicklung am Panamakanal ab. Die folgende Graphik habe ich mit meiner eigenen App erstellt. Wir erkennen, dass die Kanalbehörden sparsam mit dem verfügbaren Wasser umgehen (müssen). Der Kanal operiert mit geringerer Kapazität – aber dazu sind (mir) leider keine Daten verfügbar. Falls Du eine Quelle kennst, dann schreibe mich gerne an!
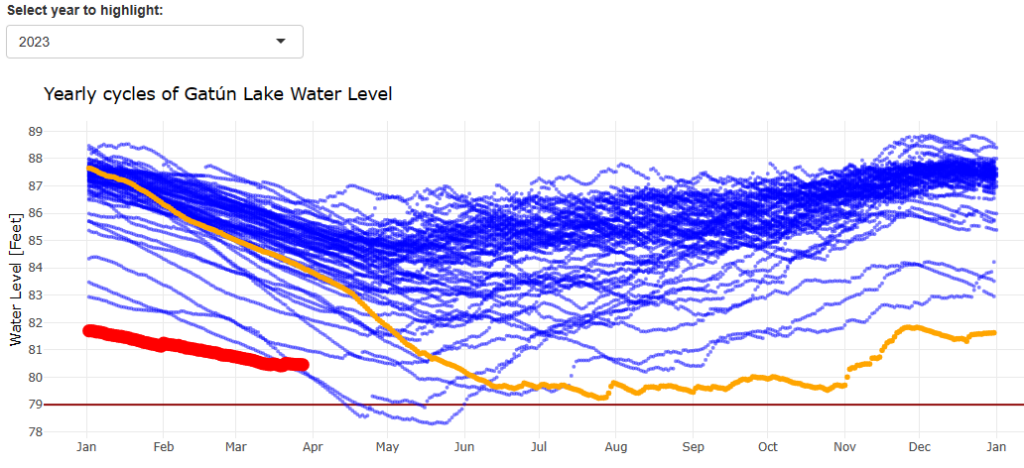
Mit der App am 28. 3. 2024 erstellter Screenshot. Hervorgehoben sind der Verlauf des Wasserstandes im Gatún-See für das Jahr 2023 (orange) und das Jahr 2024 (rot).
Es ist Frühling: die Kirschblüten blühen so schön
Wir leben in Wedel. Hier befindet sich nicht zuletzt auch die „Schiffsbegrüßungsanlage“ des Hamburger Hafens. Seit Jahrzehnten wird in Hamburg das japanische Kirschblütenfest begangen und auch wir waren zweimal in „Planten und Blomen“ dabei. Manche meiner Freunde teilen derzeit Bilder von Kirschblüten und in manchen Straßen ist es eine wahre Pracht.
Nicht umsonst also wird das Kirschblütenfest in Japan seit über 1000 Jahren begangen – und dokumentiert. Historikerinnen und Historiker haben sich durch die Quellen gearbeitet und Jahr für Jahr das Datum des Beginns der Kirschblüte veröffentlicht. Verfügbar sind ihre Daten über diese Quelle: Paleo Data Search | Study | National Centers for Environmental Information (NCEI) (noaa.gov).
Yasuuki Aono hat Daten bis hin zum Jahr 2021 zusammengetragen. Diese Daten verwende ich hier: „Historical Series of Phenological data for Cherry Tree Flowering at Kyoto City„. Wenn Du eine Quelle hast, die bis heute aktualisiert wird, dann bin ich daran interessiert – denn die Daten sind wertvoll, da sie so einen langen Zeitraum überstreichen, und es ist interessant und wichtig zu sehen, wie es weitergeht. Ich habe mir die Daten heruntergeladen, lese sie mit folgendem R-Skript ein und bereite sie auf:
# Daten einlesen:
df <- read_excel("040_KyotoFullFlowerW.xls", skip = 15)[, 1:5]
# Spaltennamen vereinfachen:
colnames(df) <- c("Year",
"DOY",
"Date.Coded",
"Source",
"Reference")
# Mit dieser Datumsinformation erstellen wir später die Graphiken:
df$Date <- make_date(year = year(Sys.Date()),
month = 1,
day = 1) + days(df$DOY - 1)
Erkennbar sind (siehe dafür die Graphik ganz unten), dass der Beginn der Kirschblüte von Jahr zu Jahr stark schwanken kann. Aber es ist auch ersichtlich, dass sie in den letzten 150 Jahren tendenziell früher begonnen hat.
Datenaufbereitung
Das möchte ich mir genauer ansehen. Dafür berechne ich Jahr für Jahr einen gleitenden Mittelwert über eine frei wählbare Zeitspanne („span“). Für die jeweilige Spanne bestimme ich ebenso die Standardabweichung. Es mag nicht besonders elegant sein (R-Profis rümpfen die Nase, wenn ich eine Schleife verwende), aber es ist eben doch auch schnell getan und so erstelle ich mir eine neue Tabelle res (wie „result“, also „Ergebnis“) wie folgt:
# Vorbereitungen:
start <- min(df$Year)
end <- max(df$Year)
span <- 20 # Über diese Spanne wird der Mittelwert ermittelt
res <- NULL # Initialisierung der Tabelle res
# Erstellung von gleitendem Mittelwert und Standardabweichungen:
for (y in (start+span):end) {
temp <- df %>%
filter(Year <= y,
Year >= y-span)
append <- data.frame(
Year = y,
Moving.Average = round(mean(temp$DOY, na.rm = TRUE), 0),
SD = sd(temp$DOY, na.rm = TRUE)
)
res <- rbind(res, append)
}
# Wir erzeugen noch einen "optisch ansprechenden "Vertrauensschlauch":
alpha <- 0.4 # frei wählbar
z <- qnorm(1 - alpha / 2) # z-Wert für 95% CI
res$LowerCI <- round(res$Moving.Average - z * res$SD, 0)
res$UpperCI <- round(res$Moving.Average + z * res$SD, 0)
res$Date <- make_date(year = year(Sys.Date()),
month = 1,
day = 1) + days(res$Moving.Average - 1)
res$Date.UCL <- make_date(year = year(Sys.Date()),
month = 1,
day = 1) + days(res$UpperCI - 1)
res$Date.LCL <- make_date(year = year(Sys.Date()),
month = 1,
day = 1) + days(res$LowerCI - 1)
So lässt sich dann folgende Graphik erzeugen:
# Zunächst die Werte selbst:
p <- ggplot() +
geom_point(data = df,
aes(x = Year,
y = Date))
# Wir fügen den "Schlauch für den Vertrauensbereich hinzu:
p <- p +
geom_ribbon(data = res,
aes(x = Year,
ymin = Date.LCL,
ymax = Date.UCL))
# Nun kommt noch der gleitende Mittelwert:
p <- p +
geom_line(data = res,
aes(x = Year,
y = Date)) +
theme_minimal()
print(p)
Mit einigen „Verschönerungen“ (siehe unten) erhalte ich das folgende Ergebnis. Da ich diese Graphik am Dienstag nach Ostern in einer Schulung für Analystinnen und Analysten verwenden werde, siehst Du mir die englische Beschriftung hoffentlich nach:
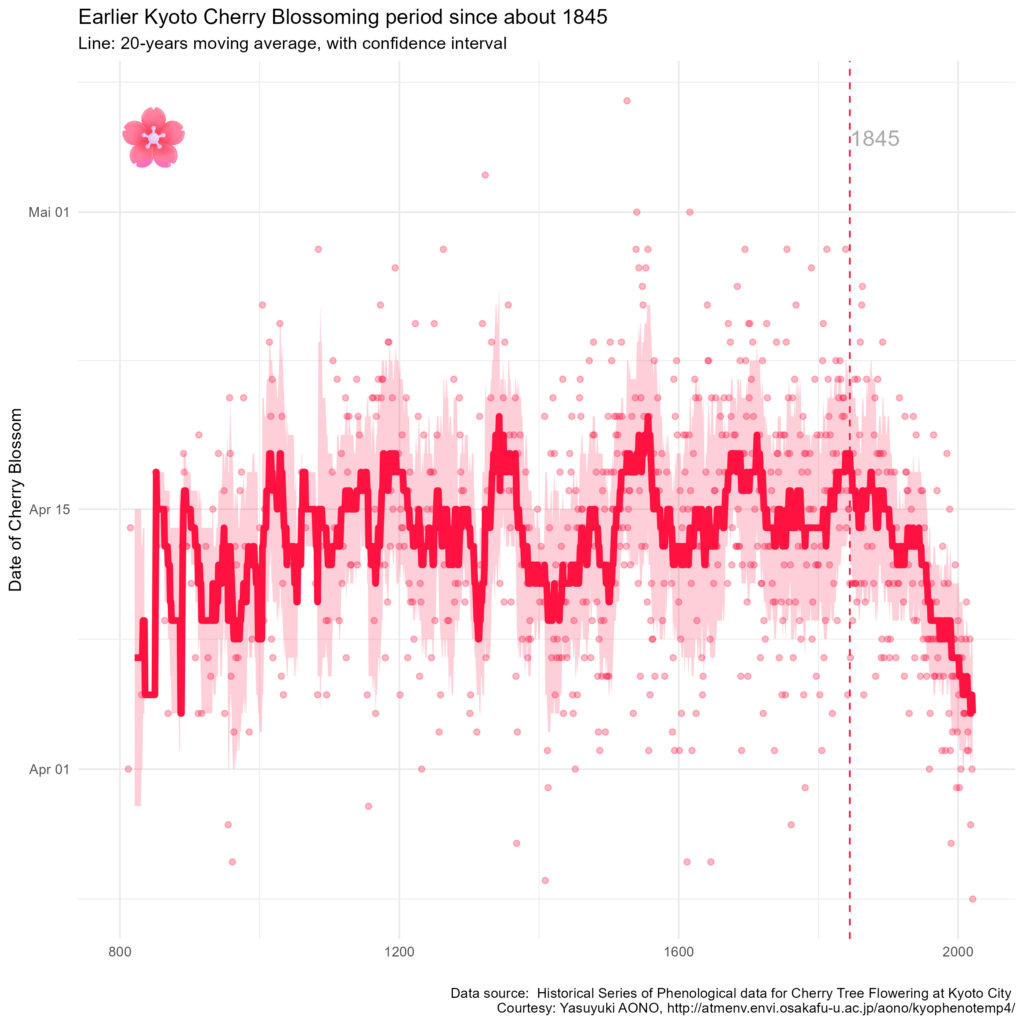
Auf der horizontalen Achse ist das jeweilige Jahr aufgetragen und auf der vertikalen Achse das Datum der ersten Kirschblüte. Jeder Punkt entspricht einem Kirschblütenfest – seit mehr als 1200 Jahren… Deutlich erkennbar ist der Trend zu immer früherer Kirschblüte seit dem Jahr 1845.
Nun bin ich zugegebenermaßen nicht der Erste, der diese Daten aufbereitet. Der Economist hat das im Jahr 2017 in seinem – in der Regel sehr lesenswerten – „Graphical Detail“ schon getan. Dort wird auch das Offensichtliche diskutiert:
Die Kirschblüte ist ein „Klimaindikator“.
Wenn es wärmer wird, dann blühen die Kirschen früher. Und seit Mitte des 19. Jahrhunderts sind weltweit die Temperaturen angestiegen.
Mir liegt hier an folgenden zwei Aspekten:
- Mit dem Panamakanal, jetzt der Kirschblüte und auch inspiriert von einem Blog meines ESSC-Kollegen Daniel Fügner zur Entwicklung des Wasserstands der Nidder denke ich, dass ich noch einige weitere „Klimaindikatoren“ aufspüren und untersuchen möchte. Damit meine ich frei verfügbare Messreihen, gerne über Jahrzehnte oder wie hier sogar Jahrtausende hinweg, die direkt oder indirekt Aufschluss über Klimaveränderungen geben können. Wenn Du Ideen oder Quellen hast: gerne!
- Beruflich bin ich immer wieder mit „kritischen“ Daten konfrontiert – und sehe, wie wenig achtsam, durchaus im modernen Sinne des Wortes, diese aufbereitet und dargestellt werden. Wenn wir mit Daten Botschaften vermitteln, vielleicht sogar Handlung inspirieren wollen, dann müssen wir diese Daten auch aufbereiten und die Botschaft auf ansprechende Weise klar herausarbeiten. Deshalb möchte ich hier auch den Code bereitstellen. Denn es liegt mir daran, diese Fähigkeiten zu „demokratisieren“.
Der vollständige Quellcode der Graphik
Ganz im Sinne des zweiten Punktes: Gerne kannst Du diese Graphik bei Dir zuhause selbst erstellen und verändern. Dieses Wissen lässt sich übrigens nur deshalb so leicht teilen, weil es hier als Skript verfügbar ist. Wenn Du diese Fähigkeit hast: versuche einmal, jemand anderem zu erklären, wie er oder sie so eine Graphik in Excel erzeugen kann…
# Read the cherry png:
cherry <- png::readPNG("cherry.png")
# TODO: replaces geom_point with cherry-pictures.
ggplot() +
annotation_custom(rasterGrob(cherry),
xmin = start,
xmax = start + 100,
ymin = as.Date("2024-05-01"),
ymax = Inf) +
geom_point(data = df,
aes(x = Year,
y = Date),
colour = "#FF1140",
alpha = 0.3,
size = 1.5) +
geom_ribbon(data = res,
aes(x = Year,
ymin = Date.LCL,
ymax = Date.UCL),
fill = "#FF1140",
alpha = 0.2) +
geom_line(data = res,
aes(x = Year,
y = Date),
linewidth = 2,
colour = "#FF1140") +
geom_vline(xintercept = 1845, colour = "#FF1140", linetype = "dashed") +
geom_text(aes(x = 1845,
y = as.Date("2024-05-05"),
label = "1845"),
vjust = 0.5, hjust = 0, color = "darkgrey", size = 5) +
theme_minimal() +
labs(title = "Earlier Kyoto Cherry Blossoming period since about 1845",
subtitle = "Line: 20-years moving average, with confidence interval",
x = "", y = "Date of Cherry Blossom",
caption = paste("Data source: ", source)
)